Умножение в столбик — как умножать в столбик в 3 и 4 класс
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
- Однозначное — состоит из одного знака
- Двузначное — из двух
- Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
- В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.
Умножение — арифметическое действие в котором участвуют два аргумента.
Свойства умножения1. От перестановки множителей местами произведение не меняется. 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым. |
Важно помнить правило: умножение в столбик с нулями дает в результате ноль
- а * 0 = 0, где а — любое натуральное число.
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
5. Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика.
Возьмем пример 234 * 2:
1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
3. Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 * 8063:
- Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
- Последовательно перемножаем значения разрядов. Результатом является неполное произведение.
- Далее перемножаем десятки.
 Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.
Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.
- По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
- Далее складываем два произведения в столбик.
- Получившееся семизначное число — результат умножения исходных натуральных чисел.
Ответ: 8 063 * 207 = 1669041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Повтори тему — деление в столбик, она очень полезная!
Чтобы запомнить все правила, повторите метод сложения столбиком, так как один из этапов умножения состоит из сложения промежуточных результатов.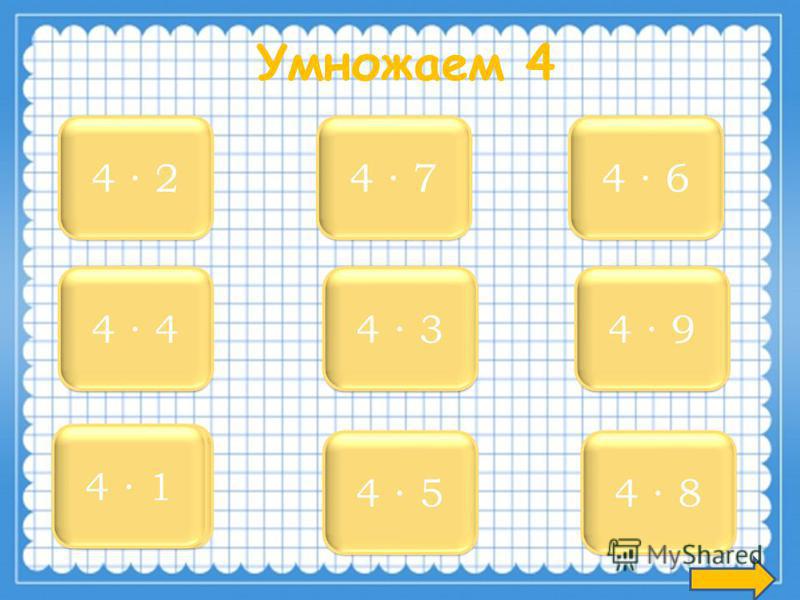 А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.
А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.
Вместо скучных параграфов ученики решают интерактивные задачки и головоломки с мгновенной автоматической проверкой, а еще чертят фигуры на онлайн-доске вместе с преподавателем.
Порядок действий
В уроке выражения мы узнали, что они бывают числовые и буквенные. Мы рассмотрели несколько числовых и буквенных выражений. Это были самые простейшие выражения.
Настало время сдвинуться с мёртвой точки и рассмотреть более сложные выражения. В данном уроке мы познакомимся с порядком выполнения действий.
Выражения могут состоять из нескольких чисел. Таковыми к примеру являются следующие выражения:
10 − 1 + 2 + 3
(3 + 5) + 2 × 3
5 × 2 + (5 − 3) : 2 + 1
Такие выражения нельзя вычислить сразу, то есть поставить знак равенства и записать значение выражения. Да и выглядят они не так просто, как 2 + 2 или 9 − 3.
Для подобных выражений принято соблюдать так называемый порядок действий
 Суть в том, что выражение вычисляется кусочками по определённому порядку.
Суть в том, что выражение вычисляется кусочками по определённому порядку.Когда нам требуется решить подобные примеры, мы сразу должны мысленно прочитать следующее правило:
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение 10 − 1 + 2 + 3. Видим, что в нём нет никаких скобок. Тогда переходим к следующему правилу, которое выглядит так:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Видим, что в нём нет никакого умножения или деления. Тогда переходим к следующему правилу:
Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию!
Читаем наше выражение 10 − 1 + 2 + 3 слева направо. Встречаем вычитание 10 − 1. Сразу выполняем эту операцию: 10 − 1 = 9. Полученную девятку запишем в главном выражении вместо 10 − 1
Затем снова читаем те, правила, которые мы прочитали выше. Читать их нужно в следующем порядке:
Читать их нужно в следующем порядке:
1. Сначала вычислить то, что находится в скобках!
2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же применяем эту операцию!
3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же применяем эту операцию!
Сейчас у нас имеется выражение 9 + 2 + 3 Читаем его слева направо и встречаем сложение 9 + 2. Выполняем эту операцию: 9 + 2 = 11. Запишем число 11 в главном выражении вместо 9 + 2:
Осталось простейшее выражение 11 + 3, которое вычисляется легко:
11 + 3 = 14
Таким образом, значение выражения 10 − 1 + 2 + 3 равно 14
10 − 1 + 2 + 3 = 14
Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 10 − 1 = 9
2) 9 + 2 = 11
3) 11 + 3 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий. Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:
Например, решение для выражения 10 − 1 + 2 + 3 можно записать следующим образом:
Но если человек не научился быстро считать в уме, то не рекомендуется использовать такой способ.
Пример 2. Найти значение выражения (3 + 5) + 2 × 3
Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
Сначала вычислить то, что находится в скобках!
Посмотрим на выражение (3 + 5) + 2 × 3. Видим, что в нём есть выражение в скобках (3 + 5). Вычислим то, что в этих скобках: 3 + 5 = 8. Запишем полученную восьмёрку в главном выражении вместо выражения в скобках:
8 + 2 × 3
Снова читаем первое правило:
Сначала вычислить то, что находится в скобках!
Видим, что в выражении 8 + 2 × 3 нет никаких скобок. Тогда читаем следующее правило:
Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию!
Посмотрим на наше выражение 8 + 2 × 3. Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3
Видим, что в нём есть умножение 2 × 3. Выполним эту операцию: 2 × 3 = 6. Запишем полученную шестёрку в главном выражении вместо 2 × 3
8 + 6
Осталось простейшее выражение 8 + 6, которое вычисляется легко:
8 + 6 = 14
Таким образом, значение выражения (3 + 5) + 2 × 3 равно 14
(3 + 5) + 2 × 3 = 14
Также, этот пример можно решить, расставив порядок действий над самим выражением. Действие в скобках будет первым действием, умножение — вторым действием, а сумма — третьим:
И далее можно выполнить действия по отдельности, что очень удобно:
1) 3 + 5 = 8
2) 2 × 3 = 6
3) 8 + 6 = 14
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Но опять же, используя такой способ, нужно быть очень внимательным.
Пример 3. Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1
Найти значение выражения 5 × 2 + (5 − 3) : 2 + 1
Расставим порядок действий над выражением. Действие в скобках будет первым действием, умножение — вторым действием, деление — третьим действием, четвёртое и пятое действие являются суммами и они будут выполнены в порядке их следования:
1) 5 − 3 = 2
2) 5 × 2 = 10
3) 2 : 2 = 1
4) 10 + 1 = 11
5) 11 + 1 = 12
Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:
Четвёртое и пятое действие заключалось в том, чтобы вычислить оставшееся простейшее выражение 10 + 1 + 1. Мы не стали тратить время на выполнение каждого из этих действий, а поставили знак равенства и записали ответ 12.
Пример 4. Найти значение выражения (3250 − 2905) : 5
Расставим порядок действий над выражением. Действие в скобках будет первым действием, а деление — вторым
Действие в скобках будет первым действием, а деление — вторым
1) 3250 − 2905 = 345
2) 345 : 5 = 69
В скобках могут выполняться два и более действия. Бывает даже так, что в скобках встречаются другие скобки. В таких случаях нужно применять те же правила, которые мы изучили ранее.
Пример 5. Найти значение выражения (6 411 × 8 − 40799) × 6
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется умножение и вычитание. Согласно порядку действий, умножение выполняется раньше вычитания.
В данном случае сначала нужно 6 411 умножить на 8, и из полученного результата вычесть 40 799. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат будет умножен на 6.
В результате будем иметь следующий порядок:
1) 6 411 × 8 = 51 288
2) 51 288 − 40 799 = 10 489
3) 10 489 × 6 = 62 934
Пример 6. Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)
Найти значение выражения: 1 657 974 : 822 × 106 − (50 377 + 20 338)
Расставим порядок действий над выражением. Действие в скобках будет первым действием, деление будет вторым действием, умножение — третьим, вычитание — четвёртым.
1) 50 377 + 20 338 = 70 715
2) 1 657 974 : 822 = 2 017
3) 2 017 × 106 = 213 802
4) 213 802−70 715 = 143 087
Пример 7. Найти значение выражения: 14 026 − (96 : 4 + 3680)
Расставим порядок действий над выражением. Действие в скобках будет первым действием. При этом в скобках выполняется деление и сложение. Согласно порядку действий деление выполняется раньше сложения.
В данном случае сначала нужно 96 разделить на 4, и полученный результат сложить с 3 680. Полученный результат будет значением выражения, содержащегося в скобках. Этот результат нужно вычесть из 14 026. В результате будем иметь следующий порядок:
1) 96 : 4 = 24
2) 24 + 3 680 = 3 704
3) 14026 − 3 704 = 10 322
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
Найдите значение выражения:
5 + 2 − 2 − 1
Решение
Задание 2. Найдите значение выражения:
14 + (6 + 2 × 3) − 6
Решение
Задание 3. Найдите значение выражения:
486 : 9 − 288 : 9
Решение
Задание 4. Найдите значение выражения:
756 : 3 : 4 × 28
Решение
Задание 5. Найдите значение выражения:
807 : 3 − (500 − 58 × 4)
Решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Урок 4. Частные методики умножения двузначных чисел до 30
Преимуществом трех способов умножения двузначных для устного счета, описанных в прошлом уроке, состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу. Однако, эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.
Однако, эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов.
В этом уроке вы узнаете, как можно быстро умножать любые числа до 30. Здесь представлены специальные методики, в том числе и введение в использование опорного числа.
Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.
Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10. Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.
Умножать на 11 таким способом можно любые двузначные числа. Для наглядности приведены примеры:
81 * 11 = 8 (8+1) 1 = 891
68 * 11 = 6 (6+8) 8 = 748
Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа — об этом читайте в данной статье, а также в книге «Система быстрого счета по Трахтенбергу».
Квадрат суммы, квадрат разности
Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:
232= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529
692 = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.
152 = (1*(1+1)) 25 = 225
252 = (2*(2+1)) 25 = 625
852 = (8*(8+1)) 25 = 7 225
Это верно и для более сложных примеров:
1552 = (15*(15+1)) 25 = (15*16)25 = 24 025
Умножение чисел до 20
1 шаг. Для примера возьмём два числа – 16 и 18. К одному из чисел прибавляем кол-во единиц второго – 16+8=24
Для примера возьмём два числа – 16 и 18. К одному из чисел прибавляем кол-во единиц второго – 16+8=24
2 шаг. Полученное число умножаем на 10 – 24*10=240
3 шаг. Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288
Методика умножения чисел до 20 очень проста:
Если записать короче, то:
16*18 = (16+8)*10+6*8 = 288
Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода.
По сути, этот метод является частным способом использования опорных чисел (о которых будет сказано в следующем уроке). В данном случае опорным числом является 10. В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку. Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100… Подробнее о методе использования опорного числа читайте в следующем уроке.
Опорное число
Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8. Для того, чтобы узнать их произведение, нужно совершить следующие операции:
- К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
- Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
- К 230 прибавляем произведение 5*8. Ответ: 270.
Подробнее о методике использования опорного числа для счета в уме читайте в следующем уроке.
Тренировка
Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.
Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.
Выбрасывай калькулятор: 17 полезных математических трюков
Собрали подборку классных математических трюков в помощь. С ними ты сможешь быстро считать в уме, не прибегая к калькулятору!
Привет!
Здесь 17 крутых математических трюков, которые полезны не только школьникам, но и взрослым. Они помогают производить сложные вычисления в голове. Освой эти техники, и будешь решать даже те задачи, которые когда-то казались непосильными.
А после можешь пройти наш быстрый математический тест 😉
Сложение крупных чисел в голове − намного более лёгкий процесс, чем кажется. А этот метод показывает, как упростить процесс, округлив все числа до десятка. Вот пример:
644 + 238
Чтобы было проще работать, округляем каждое из чисел. Итак, 644 превращаем в 650, а 238 становится 240.
Затем складываем 650 и 240. Получается 890. Чтобы найти ответ на исходное уравнение, нужно определить, сколько мы добавили к числам, чтобы их округлить.
650 — 644 = 6 и 240 — 238 = 2
Получается, что к первому числу (644) мы добавили 6, а ко второму (238) − 2. Складываем 6 и 2 вместе, получаем 8.
Остаётся вычесть из суммы округлённых чисел (890) лишнее (8):
890 — 8 = 882
Получаем, что 644 + 238 = 882. Это один из основных математических трюков, которые стоит знать.
Вот основное правило вычитания большого числа из 1000: раздели своё трёхзначное число на первую, вторую, третью цифру. Теперь вычти первую из 9, вторую из 9, а третью из 10. Например:
1000 — 556
Шаг 1: вычитаем 5 из 9 = 4
Шаг 2: вычитаем 5 из 9 = 4
Шаг 3: вычитаем 6 из 10 = 4
Ответ 444.
Умножая число 5 на четное число, можно быстро найти ответ. Например, 5 х 4:
Шаг 1: Берём число, которое хотим умножить на 5 и делим его пополам. В нашем случае, 4 превращаем в 2.
Шаг 2: Добавляем ноль к получившемуся числу, чтобы найти ответ.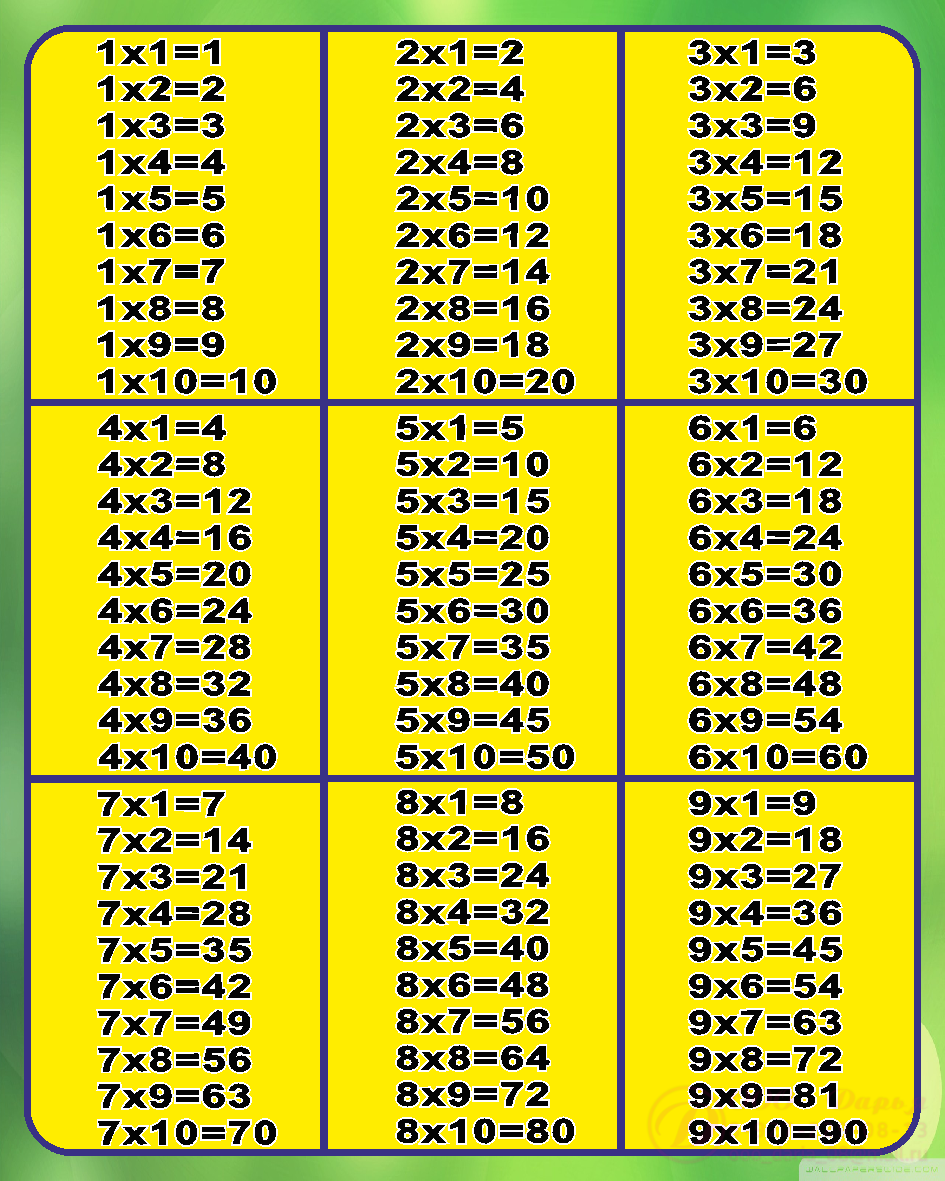 К числу 2 ставим рядом 0, получаем 20.
К числу 2 ставим рядом 0, получаем 20.
5 х 4 = 20
При умножении нечетного числа на 5 формула немного отличается. Например, рассмотрим 5 х 3:
Шаг 1: Вычитаем единицу из числа, которое хотим умножить на 5. В нашем случае, 3 превращаем в 2.
Шаг 2: Теперь делим получившееся число (2) пополам, получаем 1. Ставим последнее получившееся число на первое место, а число 5, на которое мы хотели умножать изначально, приставляем рядом. Получается, рядом с 1 ставим 5, становится 15.
5 х 3 = 15
Вот быстрый способ узнать, когда число может быть равномерно разделено на эти же числа:
- 10, если число заканчивается на 0.
- 9, когда цифры складываются вместе, а сумма делится поровну на 9.
- 8, если последние три цифры делятся на 8, или число оканчивается на 000.
- 6, если при сложении чётных чисел сумма делится на 3.
- 5, если число заканчивается на 0 или 5.
- 4, если число оканчивается на 00 или двузначное число, которое делится на 4.

- 3, если при сложении цифр числа результат делится на 3.
- 2, если оно заканчивается на 0, 2, 4, 6 или 8.
Это ещё один из математических трюков, который полезен в жизни. Нужен он для умножения любого числа на 9. Вот как это работает:
Покажем на примере умножения 9 на 3.
Шаг 1: Вычитаем 1 из числа, которое умножается на 9.
3 — 1 = 2
Число 2 является первым числом в ответе на уравнение.
Шаг 2: Вычитаем получившееся число из 9.
9 — 2 = 7
Число 7 является вторым числом в ответе на уравнение.
Итого, 9 х 3 = 27.
Хитрость в умножении любого числа на 10 состоит в добавлении нуля к концу числа. Например, 62 х 10 = 620.
Существует также простой способ умножения любого двузначного числа на 11. Вот оно:
11 х 25
Возьмём двузначное число и отделим первую часть числа от второй − из 25 сделаем 2 и 5.
Теперь складываем эти два числа вместе и помещаем результат в центр, между 2 и 5:
2 (2 + 5) 5
2 7 5
Ответ: 11 х 25 = 275.
Если число в центре содержит две цифры, добавь первое число из суммы к первой цифре итогового числа, а второе оставь на месте. Вот пример для уравнения 11 х 88:
8 (8 + 8) 8
8 (16) 8
(8 + 1) 6 8
9 6 8
Получаем ответ: 11 х 88 = 968.
Найти процент от числа может быть несколько сложно, если не подумать о способе решения, а просто считать. С этим методом всё проще. Чтобы узнать, сколько составляет 5% от 235, нужно:
Шаг 1: Переместить десятичную точку на одно значение вправо, 235 (235.0): становится 23.5.
Шаг 2: Разделить 23.5 на число 2, ответ − 11.75. Это ответ на исходное уравнение.
Используем число 35 в качестве примера:
Шаг 1: Умножим первую цифру на сумму единицы и первой цифры.
Шаг 2: В окончание поставим 25.
35 в квадрате = 3 x (3 + 1) & 25
3 x (3 + 1) = 12
12 и 25 = 1225
35 в квадрате = 1225.
Если при умножении больших чисел одно из них является четным, раздели первое число пополам, а второе умножь на 2. Например 20 х 120:
Шаг 1: Делим 20 на 2, получаем 10. Умножаем 120 на 2, получаем 240.
Затем умножаем два ответа вместе:
10 х 240 = 2400
Ответ: 20 х 120 = 2400.
Суть метода в том, чтобы умножить числа без 0, а потом добавить нули. Рассмотрим умножение 200 на 400:
Шаг 1: Умножаем первые числа − 2 на 4:
2 х 4 = 8
Шаг 2: Ставим рядом убранные нули:
80000
200 х 400 = 80000
Это похоже на метод со сложением − здесь тоже нужно округлять. Рассмотрим его на примере выражения 97 x 96:
Округлим каждое из чисел до 100. Получим 100 и 100.
Теперь из первых 100 вычитаем первое число (97) и получаем 3, из вторых 100 вычитаем второе число (96) и получаем 4. Складываем получившиеся числа:
3 + 4 = 7
Теперь из 100 вычитаем 7: получается 93. Это будут первые две цифры итогового результата. Чтобы получить оставшиеся две цифры, нужно не сложить, а умножить 3 и 4. Приписываем результат 12 к 93, получается 9312.
Это будут первые две цифры итогового результата. Чтобы получить оставшиеся две цифры, нужно не сложить, а умножить 3 и 4. Приписываем результат 12 к 93, получается 9312.
Посмотри на свои руки (в идеальном случае, должно быть 10 пальцев). Представим, что ты хочешь умножить 7 на 8.
Из 10 (как и пальцев на руках) вычти первое число (7), осталось 3. Запомни это число. Теперь вычти из 10 второе число (8), получается 2.
Теперь сложи получившиеся числа, результат (5) поставь на первое место. Затем, перемножь 3 и 2. Получится 6, цифру ставим на второе место, получается 56.
Казалось бы, как подборка математических трюков может помочь в таком серьёзном деле, как инвестирование? Может!
Если ты хочешь утроить свои инвестиции, запомни число 115. К примеру, инвестиции, которые дают 5% в год, утроятся через 23 года − 115 : 5 = 23.
Хотим посчитать 51 х 51. Возьмём одну из цифр, например, 1, к ней прибавим 25. Получается 26.
Получается 26.
Теперь перемножим ту же цифру (1), получим 1 (01).
Соединим получившееся, 26 ставим первым числом, 01 вторым. Получается 2601.
Найти корень из таких чисел, как 49 или 81 достаточно просто, потому что корни являются целыми числами. Но как можно найти корень с остатком? Покажем на примере числа 420.
Шаг 1: Находим ближайшее число, которое можно получить возведением в квадрат. В данном случае, это число 400, которое получают возведением в квадрат числа 20.
Шаг 2: Делим наше число (420) на корень того, ближайшего числа (20). Получаем 21.
Шаг 3: Теперь находим среднее между результатом и корнем первого числа − среднее между 21 и 20 равно 20,5.
А корень числа 420 равен 20,494. Получается, что наш ответ максимально близок.
Допустим, мы хотим узнать, чему равно 81 в квадрате.
81 х 81 = ?
Округляем число до меньшего − 80, возводим его в квадрат. Получается 6400.
Теперь к сумме дважды прибавляем округленное число − 6400 + 80 + 80, а в конце добавляем ещё один.
Получается 6560 + 1 = 6561.
Как бы ты посчитал значение выражения 32 х 125? Лучше упростить его:
32 х 125 = ?
16 х 250 = ?
8 х 500 = ?
4 х 1000 = 4000
На этом наша подборка математических трюков заканчивается. Практика этих быстрых математических приемов может помочь как в жизни, так и в работе. А ещё, может быть, пробудит интерес к математике.
Понравилась подборка математических трюков? Тебя точно заинтересует следующее:
Источник: 10 математических трюков в блоге Concorida University-Portland
Расскажи, какими математическими трюками пользуешься ты?
Урок 37. умножение суммы на число. приёмы умножения для случаев вида 23 ∙ 4, 4 ∙ 23 — Математика — 3 класс
Математика, 3 класс
Урок № 37. Умножение суммы на число. Приёмы умножения для случаев вида 23 ∙ 4, 4 ∙ 23
Перечень вопросов, рассматриваемых в теме:
- Как умножить двузначное число на однозначное?
- Как представить двузначное число в виде суммы разрядных слагаемых?
- В каких случаях умножения использовать приём?
Глоссарий по теме:
Умножение – это сложение одинаковых слагаемых
Сложение – это математическое действие, при котором складываем части и получаем целое.
Сумма – это результат действия сложения, а также выражение действия сложения
Обязательная литературы и дополнительная литература:
- Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для
общеобразовательных организаций М.; Просвещение, 2017. – с.6.
- Математика. 2 класс. Часть 3 / Л. Г. Петерсон. – М.: Ювента, 2013 – 96 с.: ил. с 69.
Теоретический материал для самостоятельного изучения
Мы знаем, что
прямоугольник — это геометрическая фигура, у которой все углы прямые и противоположные стороны равны.
Вспомним, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. 5 ∙ 3 = 15 см²
Как найти площадь двух прямоугольников?
1 способ
Можно умножить каждое слагаемое на это число и результаты сложить.
(5 + 3) ∙ 2 = 5 ∙ 2 + 3 ∙ 2 = 10 + 6 = 16
2 способ
Можно найти значение суммы и результат умножить на число
(5 + 3) ∙ 2 = 8 ∙ 2 = 16
Умножить сумму на число можно двумя способами.
При решении задач можно выбрать наиболее удобный.
Сумму чисел можно заменить одним числом.
Запись 23 ∙ 4 = 4 ∙ 23 представляет собой переместительное свойство умножения.
Вывод:
Ответим на вопросы, поставленные в начале урока.
Чтобы умножить сумму на число можно умножить каждое слагаемое на это число и результаты сложить. Это первый способ.
Второй способ: можно найти значение суммы и результат умножить на число.
Для удобства число представляют как сумму разрядных слагаемых.
Выполним тренировочные задания:
1) К каждому выражению первого столбца подберите соответствующее произведение.
Умножение суммы на число | Соответствующее произведение |
(10 + 6) ∙ 4 | 15 ∙ 3 |
(8 + 10) ∙ 2 | 16 ∙ 4 |
(10 + 5) ∙ 3 | 18 ∙ 2 |
Ответ: (10 + 6) ∙ 4 = 16 ∙ 4; (8 + 10) ∙ 2 = 18 ∙ 2; (10 + 5) ∙ 3 = 15 ∙ 3.
2) Выделите цветом выражение с ответом 50:
36 : 4 + 21 | 7 ∙ 8 – 42 : 7 | 20 ∙ 5 : 2 |
Ответ: 7 ∙ 8 – 42 : 7; 20 ∙ 5 : 2.
3) Вставьте пропущенные числа, выбирая из списка правильные ответы:
1. (40 + 5) ∙ 2 = ___ ∙ 2
2. (20 + 6) ∙ 3 = ___ ∙ 3
Числа на выбор: 42; 45; 20; 26; 23;
Ответ: 1) 45; 2) 26.
4) Решите задачу: Три класса посадили в школьном саду каждый по 6 акаций и по 4 берёзы. Сколько всего деревьев посадили ребята?
Решение: (6 + 4) ∙ 3 = 30 (дер.)
Ответ: 30 деревьев
Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней
Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для решения задач по теории вероятности, геометрии и математике! Также на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1 | 21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024 | 31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049 | 41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576 | 51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625 |
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176 | 71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249 | 81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824 | 91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401 | 101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000 |
Остались вопросы?
Здесь вы найдете ответы.x=3 log2(3)=x
90 в 10 степени
90 в 10 =34867844009999998976.00000
12 в степени 1/3
Сложная формула но в кратце ответ — 6
Слишком сложно?
Таблица степеней не по зубам? Тебе ответит эксперт через 10 минут!
📝Таблица чисел от 1 до 25 в степени от 1 до 10
При решении разных математических упражнений часто приходится заниматься возведением числа степень, в основном от 1 до 10. И для того, что бы быстрее находить эти значения и нами создана таблицу степеней по алгебре, которую я опубликую на этой странице.
Также у нас вы можете посмотреть таблицы квадратов и кубов.
Для начала рассмотрим числа от 1 до 6. Результаты здесь ещё не очень большие все из них вы можете проверить на обычном калькуляторе.
- 1 и 2 в степени от 1 до 10
11= 1
12= 1
13= 1
14= 1
15= 1
16= 1
17= 1
18= 1
19= 1
110= 121= 2
22= 4
23= 8
24= 16
25= 32
26= 64
27= 128
28= 256
29= 512
210= 1 024 - 3 и 4 в степени от 1 до 10
3 1 = 3
3 2 = 9
3 3 = 27
3 4 = 81
3 5 = 243
3 6 = 729
3 7 = 2 187
3 8 = 6 561
3 9 = 19 683
3 10 = 59 0494 1 = 4
4 2 = 16
4 3 = 64
4 4 = 256
4 5 = 1 024
4 6 = 4 096
4 7 = 16 384
4 8 = 65 536
4 9 = 262 144
4 10 = 1 048 576 - 5 и 6 в степени от 1 до 10
5 1 = 5
5 2 = 25
5 3 = 125
5 4 = 625
5 5 = 3 125
5 6 = 15 625
5 7 = 78 125
5 8 = 390 625
5 9 = 1 953 125
5 10 = 9 765 6256 1 = 6
6 2 = 36
6 3 = 216
6 4 = 1 296
6 5 = 7 776
6 6 = 46 656
6 7 = 279 936
6 8 = 1 679 616
6 9 = 10 077 696
6 10 = 60 466 176 - 7 и 8 в степени от 1 до 10
7 1 = 7
7 2 = 49
7 3 = 343
7 4 = 2 401
7 5 = 16 807
7 6 = 117 649
7 7 = 823 543
7 8 = 5 764 801
7 9 = 40 353 607
7 10 = 282 475 2498 1 = 8
8 2 = 64
8 3 = 512
8 4 = 4 096
8 5 = 32 768
8 6 = 262 144
8 7 = 2 097 152
8 8 = 16 777 216
8 9 = 134 217 728
8 10 = 1 073 741 824 - 9 и 10 в степени от 1 до 10
9 1 = 9
9 2 = 81
9 3 = 729
9 4 = 6 561
9 5 = 59 049
9 6 = 531 441
9 7 = 4 782 969
9 8 = 43 046 721
9 9 = 387 420 489
9 10 = 3 486 784 40110 1 = 10
10 2 = 100
10 3 = 1 000
10 4 = 10 000
10 5 = 100 000
10 6 = 1 000 000
10 7 = 10 000 000
10 8 = 100 000 000
10 9 = 1 000 000 000
10 10 = 10 000 000 000 - 11 и 12 в степени от 1 до 10
11 1 = 11
11 2 = 121
11 3 = 1 331
11 4 = 14 641
11 5 = 161 051
11 6 = 1 771 561
11 7 = 19 487 171
11 8 = 214 358 881
11 9 = 2 357 947 691
11 10 = 25 937 424 60112 1 = 12
12 2 = 144
12 3 = 1 728
12 4 = 20 736
12 5 = 248 832
12 6 = 2 985 984
12 7 = 35 831 808
12 8 = 429 981 696
12 9 = 5 159 780 352
12 10 = 61 917 364 224 - 13 и 14 в степени от 1 до 10
13 1 = 13
13 2 = 169
13 3 = 2 197
13 4 = 28 561
13 5 = 371 293
13 6 = 4 826 809
13 7 = 62 748 517
13 8 = 815 730 721
13 9 = 10 604 499 373
13 10 = 137 858 491 84914 1 = 14
14 2 = 196
14 3 = 2 744
14 4 = 38 416
14 5 = 537 824
14 6 = 7 529 536
14 7 = 105 413 504
14 8 = 1 475 789 056
14 9 = 20 661 046 784
14 10 = 289 254 654 976 - 15 и 16 в степени от 1 до 10
15 1 = 15
15 2 = 225
15 3 = 3 375
15 4 = 50 625
15 5 = 759 375
15 6 = 11 390 625
15 7 = 170 859 375
15 8 = 2 562 890 625
15 9 = 38 443 359 375
15 10 = 576 650 390 62516 1 = 16
16 2 = 256
16 3 = 4 096
16 4 = 65 536
16 5 = 1 048 576
16 6 = 16 777 216
16 7 = 268 435 456
16 8 = 4 294 967 296
16 9 = 68 719 476 736
16 10 = 1 099 511 627 776 - 17 и 18 в степени от 1 до 10
17 1 = 17
17 2 = 289
17 3 = 4 913
17 4 = 83 521
17 5 = 1 419 857
17 6 = 24 137 569
17 7 = 410 338 673
17 8 = 6 975 757 441
17 9 = 118 587 876 497
17 10 = 2 015 993 900 44918 1 = 18
18 2 = 324
18 3 = 5 832
18 4 = 104 976
18 5 = 1 889 568
18 6 = 34 012 224
18 7 = 612 220 032
18 8 = 11 019 960 576
18 9 = 198 359 290 368
18 10 = 3 570 467 226 624 - 19 и 20 в степени от 1 до 10
19 1 = 19
19 2 = 361
19 3 = 6 859
19 4 = 130 321
19 5 = 2 476 099
19 6 = 47 045 881
19 7 = 893 871 739
19 8 = 16 983 563 041
19 9 = 322 687 697 779
19 10 = 6 131 066 257 80120 1 = 20
20 2 = 400
20 3 = 8 000
20 4 = 160 000
20 5 = 3 200 000
20 6 = 64 000 000
20 7 = 1 280 000 000
20 8 = 25 600 000 000
20 9 = 512 000 000 000
20 10 = 10 240 000 000 000 - 21 и 22 в степени от 1 до 10
21 1 = 21
21 2 = 441
21 3 = 9 261
21 4 = 194 481
21 5 = 4 084 101
21 6 = 85 766 121
21 7 = 1 801 088 541
21 8 = 37 822 859 361
21 9 = 794 280 046 581
21 10 = 16 679 880 978 20122 1 = 22
22 2 = 484
22 3 = 10 648
22 4 = 234 256
22 5 = 5 153 632
22 6 = 113 379 904
22 7 = 2 494 357 888
22 8 = 54 875 873 536
22 9 = 1 207 269 217 792
22 10 = 26 559 922 791 424 - 23 и 24 в степени от 1 до 10
23 1 = 23
23 2 = 529
23 3 = 12 167
23 4 = 279 841
23 5 = 6 436 343
23 6 = 148 035 889
23 7 = 3 404 825 447
23 8 = 78 310 985 281
23 9 = 1 801 152 661 463
23 10 = 41 426 511 213 64924 1 = 24
24 2 = 576
24 3 = 13 824
24 4 = 331 776
24 5 = 7 962 624
24 6 = 191 102 976
24 7 = 4 586 471 424
24 8 = 110 075 314 176
24 9 = 2 641 807 540 224
24 10 = 63 403 380 965 376 - 25 в степени от 1 до 10
25 1 = 25
25 2 = 625
25 3 = 15 625
25 4 = 390 625
25 5 = 9 765 625
25 6 = 244 140 625
25 7 = 6 103 515 625
25 8 = 152 587 890 625
25 9 = 3 814 697 265 625
25 10 = 95 367 431 640 625
Хочу напомнить:
Для того, что бы возвести число «a» в степень «b» надо «a» умножить само на себя «b» раз!
Вот, например, в начале изучения компьютера мы рассматриваем двоичный код – то есть язык, на котором «разговаривает» компьютер. И там часто используются разные степени двойки, которые надо знать. От вы знаете, сколько будет два в восьмой?
Материалы по теме:
Поделиться с друзьями:
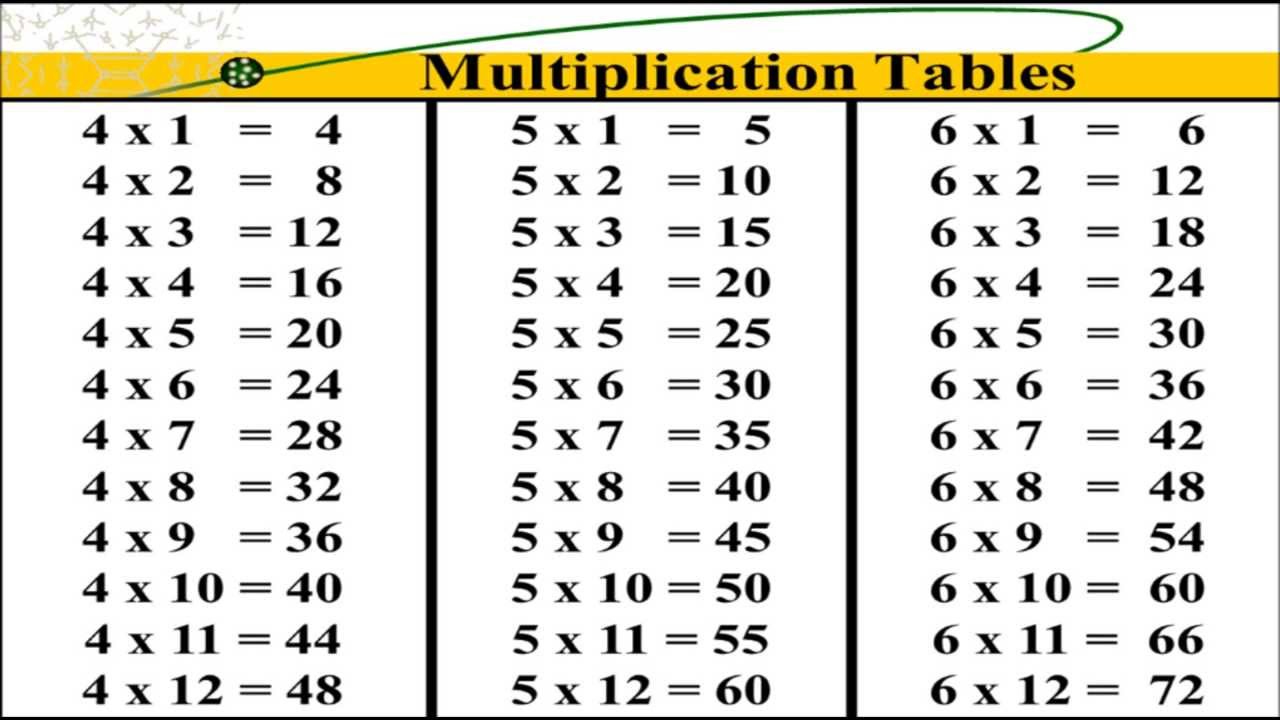
Загрузка…Умножение на 8 — 3 класс по математике
Научитесь умножать на 8
В этом уроке вы научитесь умножать на 8.
Но что значит умножение на 8?
Умножение — повторное сложение.
Допустим, вы пригласили 8 друзей поиграть.
Вы думаете о выпечке печенья.
Если вы хотите, чтобы у каждого друга было по 3 куки, сколько куки вам нужно приготовить?
Вы найдете ответ, если умножите на 8.😀
Умножение на 8 аналогично подсчету пропусков на 8 раз. Или вы также можете представить это как добавление 8 равных групп.
Так что же 8 x 3?
Давайте пропустим счет 3, восемь раз:
3, 6, 9, 12, 15, 18, 21, 24
Итак, 8 x 3 = 24!
🤓 Совет: , если подсчет пропусков по одному коэффициенту слишком сложен, попробуйте другой коэффициент.
Давайте попробуем пропустить счет на 8, трижды:
8, 16, 24!
Снова мы видим, что 8 x 3 = 24!
Разве не полезно знать, как умножить на 8?
Умножение на 8
Это таблица умножения на 8.
Вы заметили узор?
Посмотрите ответы от 1 до 10.
😀 Цифры в разряде Единиц уменьшаются на 2.
Начинается с 8 и идет вниз до 0.
Затем он снова начинается с 8 и снова снижается до 0.
Вы заметили другой узор?
Верно!
😀 Все ответы — четных чисел.
Секретный трюк
Возможно, вы впервые попытаетесь умножить на 8.
Вы можете подумать, что это сложно, но на самом деле это не так.
Вот секретный трюк, который поможет упростить умножение на 8. 😎
Когда вам нужно умножить на 8, просто удвоить число 3 раза.
Удвоение числа означает умножение на 2.
Это работает, потому что 2 x 2 x 2 = 8!
Допустим, вам нужно умножить это:
4 x 8 = ?
👉 Сначала умножьте 4 на 2.
4 x 2 = 8
👉 Затем умножьте свой ответ еще раз на 2.
8 x 2 = 16
👉 Наконец, умножьте свой ответ на 2 в третий раз.
16 x 2 = 32
Последний номер, который вы получите, и есть ваш ответ.
32! 🚑
Давайте попробуем другой пример.
Умножьте это:
8 x 5 = ?
Что вы ответите?
Отличная работа!
Это 40! 😀
Каким способом вы нашли ответ? 😎
Помните, что таблица умножения — ваш самый полезный инструмент.
Смотри и учись
А теперь пора попробовать попрактиковаться. 💪
Калькулятор умножения дробей
Как умножать дроби?
Умножение дробей (или любых других чисел или переменных) может обозначаться знаком умножения × между двумя дробями, точкой между двумя дробями или круглыми скобками вокруг одной или обеих дробей.Например,
$$ \ frac {8} {3} \ times \ frac {7} {2}, \ quad \ frac {8} {3} \ cdot \ frac {7} {2}, \ quad \ Big (\ frac {8} {3} \ Big) \ frac {7} {2}, \ quad \ frac {8} {3} \ Big (\ frac {7} {2} \ Big), \ quad \ Big (\ frac {8} {3} \ Big) \ Big (\ frac {7} {2} \ Big) $$
Результат умножения — это произведение. Когда мы имеем дело с умножением дробей, существует три типа умножения.
Умножение дроби на дробь
Чтобы умножить две или более дроби, умножьте их числители и умножьте их знаменатели.Если дроби имеют общие множители в числителях и знаменателях, упростите их перед умножением. Например, произведение двух дробей `a / b` и` c / d` для `b, d \ ne0` равно
$$ \ frac {a} {b} \ times \ frac {c} {d } = \ frac {a \ times c} {b \ times d}, \ quad b, d \ ne0 $$
Поэтому для умножения двух и более дробей необходимо выполнить три шага:
- Умножаем числители;
- Умножить знаменатели;
- При необходимости упростите продукт.
$$ \ frac {8} {3} \ times \ frac {7} {2} = \ frac {8 \ times7} {3 \ times2} = \ frac {56} {6} $$
Чтобы записать произведение в простейшей форме, найдите GCF числителя и знаменателя произведения. GCF 56 и 6 равен 2. После деления числителя и знаменателя на GCF мы получаем
. $$ \ frac {56} {6} = \ frac {56: 2} {6: 2} = \ frac {27} {3} $$
Умножить дробь на целое число
Поскольку целое число можно переписать как само деленное на 1, мы можем применить предыдущее правило умножения дроби на другую дробь.Следовательно, произведение дроби `a / b`,` b \ ne0` и целого числа c может быть записано следующим образом
$$ \ frac a b \ times c = \ frac a b \ times \ frac {c} {1} $$
Умножение смешанных чисел
Чтобы умножить смешанные числа, преобразуйте их в неправильные дроби, а затем умножьте дроби. Например, умножим дроби `2 \ frac {2} {3}` и `\ frac {7} {2}`. Поскольку `2 \ frac {2} {3}` равно `\ frac {8} {3}`, мы продолжаем шаги умножения с дробями `\ frac {8} {3}` и `\ frac {7} { 2} `в соответствии с первым случаем.
Аналогичное соображение можно применить к умножению алгебраических дробей.
Работа умножения дробей с шагами показывает полное пошаговое вычисление для нахождения произведения двух дробей «8/3» и «7/2» с использованием правила умножения. Для любых других дробей просто укажите две правильные или неправильные дроби и нажмите кнопку «Создать работу». Учащиеся начальной школы могут использовать этот калькулятор умножения дробей для создания работы, проверки результатов умножения чисел, полученных вручную, или для эффективного выполнения домашних заданий.
Умножение × | Основы арифметики
На этой странице описаны основы умножения (×) .
См. Другие наши арифметические страницы для обсуждения и примеров: Сложение (+), Вычитание (-) и Деление ( ÷ ).
Умножение
При записи общий знак умножения — « × ». В электронных таблицах и некоторых других компьютерных приложениях символ « * » (или звездочка) используется для обозначения операции умножения.
Чтобы выполнять вычисления умножения без калькулятора или электронной таблицы, вам необходимо знать, как складывать числа. См. Нашу страницу добавления, чтобы узнать, как добавить.
Когда вы «умножаете» или «умножаете» число, вы прибавляете его к самому себе несколько раз, например, умножение 4 на 3 — это то же самое, что сказать 4 + 4 + 4 = 12. Следовательно, умножение — это более быстрый способ сложения одно и то же число много раз, например 3 × 4 = 12. Этот расчет аналогичен выражению, если у меня есть 3 пакета по 4 яблока, сколько всего яблок у меня есть?
Основные правила умножения:
- Любое число, умноженное на 0, равно 0.200 × 0 = 0
- Любое число, умноженное на 1, остается неизменным. 200 × 1 = 200.
- Когда число умножается на два, мы удваиваем число. 200 × 2 = 400.
- Когда целое число умножается на 10, мы можем просто написать 0 в конце (один ноль из 10, потому что это 1 × 10). 200 × 10 = 2000.
- При умножении на 100 мы записываем два нуля в конце, на тысячу записываем три нуля в конце и так далее. Например, 4 × 2000 — это 4 × 2 = 8 с 3 нулями: 8000.
Для простого и быстрого умножения полезно запомнить умножение или «таблицу умножения », как показано ниже. Эта таблица дает ответы на все умножения до 10 × 10. Чтобы получить ответ на 4 × 6, например, найдите 4 в верхней (заштрихованной красным) строке и найдите 6 в левом (заштрихованном красным) столбце — столбец точка пересечения двух линий и есть ответ: 24 .
Неважно, в каком направлении вы ищите числа; если вы найдете 4 в первом столбце и 6 в первой строке, вы получите тот же ответ, 24.
Таблица умножения
| × | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Приведенная выше таблица может помочь нам быстро вычислить ответ на следующую проблему.Меган ведет трех братьев в кинотеатр, ей нужно купить всего 4 билета, каждый из которых стоит 8 фунтов стерлингов. Во сколько обойдется поездка? Нам нужно вычислить 4 лота по 8 фунтов стерлингов, что написано 4 × 8.
Найдите 4 в вертикальном красном столбце и 8 в горизонтальном красном столбце, ответ находится в ячейке, где пересекаются две линии: 32 . Стоимость похода в кинотеатр составит 32 фунтов стерлингов.
Часто бывает необходимо умножать числа больше 10.В этом случае приведенная выше таблица умножения не может дать немедленного ответа. Однако мы все еще можем использовать его, чтобы упростить расчет.
Лиза занимается ресторанным бизнесом. Она должна доставить бутерброды 23 предприятиям, в каждом из которых работает 14 сотрудников. Если предположить, что каждый сотрудник съедает один бутерброд, сколько бутербродов нужно приготовить Лизе?
23 предприятиям требуется 14 бутербродов, что составляет 23 лота по 14 или, другими словами, 23, умноженные на 14. Как мы уже обнаружили, мы можем записать расчет наоборот.14 × 23. Ответ будет таким же.
Нам нужно найти ответ на расчет 23 × 14.
Сначала запишите свои числа в столбцы, представляющие сотни, десятки и единицы (за помощью см. Нашу страницу Числа ).
| Сот | Десятки | Шт. |
| 2 | 3 | |
| 1 | 4 |
Шаг 1: Начиная с правого столбца (единицы), умножьте 4 и 3.При необходимости вы можете обратиться к приведенной выше таблице умножения. Напишите ответ (12) под своим вычислением, стараясь поставить 1 в столбце десятков и 2 в столбце единиц.
Синие числа — это те, над которыми мы сейчас работаем, а розовые числа — это первая часть нашего ответа.
| Сот | Десятки | Шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 |
Шаг 2: Затем мы умножаем 4 на следующее число, равное 2 (или 20, потому что оно находится в столбце десятков).Напишите свой ответ внизу в столбце десятков: мы пишем 8 в столбце десятков (4 раза по 2 десятка) и ноль в столбце единиц (4 раза по 2 десятка это то же самое, что 4 × 20 = 80).
| Сот | Десятки | Шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 |
Шаг 3: В приведенных выше шагах мы умножили единицы нижнего числа (4) на верхнее число (23).Затем нам нужно умножить десятки в нижнем числе (1) на верхнее число (23). Теперь мы работаем с цифрой в столбце десятков нижнего числа и повторяем шаги, описанные выше. Оглядываясь на наши основные правила умножения, приведенные выше, мы знаем, что, умножая число на 10, мы пишем ноль в конце. На этом этапе, поскольку мы переместились по столбцу и работаем с десятками, мы должны не забыть записать нули в первый столбец (единицы).
Выполните 1 × 3. Как и выше, мы записываем наш ответ (3) в столбец десятков и (0) в столбец единиц.
| Сот | Десятки | Шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 |
Шаг 4: Последнее умножение, которое нам нужно выполнить, — 1 × 2.Оба числа находятся в столбце десятков, поэтому мы умножаем один лот из 10 на два лота по 10. Используя правила, которые мы узнали на предыдущих шагах, нам нужно записать ноль в столбец единиц и , ноль столбец десятков. Наш ответ (1 × 2 = 2) записан в столбце сотен, потому что мы фактически вычислили 10 × 20 = 200.
| Сот | Десятки | Шт. |
| 2 | 3 | |
| 1 | 4 | |
| 1 | 2 | |
| 8 | 0 | |
| 3 | 0 | |
| 2 | 0 | 0 |
Этап 5: На этом этапе мы закончили умножение; остается только сложить все наши ответы (розовые числа), чтобы найти общее количество необходимых бутербродов.См. Нашу страницу Дополнение , если вам нужна помощь с суммированием чисел.
| Сот | Десятки | Шт. | |
| 2 | 3 | ||
| 1 | 4 | ||
| 1 | 2 | ||
| 8 | 0 | ||
| 3 | 0 | ||
| 2 | 0 | 0 | |
| Всего: | 3 | 2 | 2 |
12 + 80 + 30 + 200 = 322. Мы подсчитали, что Лизе нужно сделать в общей сложности 322 бутербродов.
В приведенном выше примере показано, как выполнить умножение, разделенное на все возможные части, но по мере повышения уверенности можно пропустить шаги.
Можно, например, умножить 4 на 23, разбив полученную сумму:
4 × 20 = 80
4 × 3 = 12
80 + 12 = 92
| Сот | Десятки | Шт. |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 |
То же для второго столбца:
10 × 23 = 230
| Сот | Десятки | Шт. |
| 2 | 3 | |
| 1 | 4 | |
| 9 | 2 | |
| 2 | 3 | 0 |
Наконец, мы складываем два наших ответа:
| Сот | Десятки | Шт. | |
| 2 | 3 | ||
| 1 | 4 | ||
| 9 | 2 | ||
| 2 | 3 | 0 | |
| Всего: | 3 | 2 | 2 |
92 + 230 = 322.
Умножение более двух чисел
Если вам нужно перемножить более двух элементов, обычно проще перемножить первые два элемента, получить сумму, а затем умножить следующее число на первую сумму. Например, если Джо хотел вычислить, сколько часов он проработал за четырехнедельный период, то расчет выглядел бы так:
Джо работает 7 часов в день 5 дней в неделю в течение четырех недель.
Шаг первый:
7 × 5 = 35 (количество часов, которые Джо работает за одну неделю).
Шаг второй:
Чтобы узнать, сколько часов Джо работает за четыре недели, мы можем затем умножить этот ответ (35) на 4. 35 × 4 = 140.
Если мы знаем, что Джо платят 12 фунтов в час, мы можем затем подсчитать, сколько денег он заработал за четырехнедельный период: 12 × 140.
Быстрый способ решить это — вычислить:
10 × 140 = 1400 (помните, что если мы умножаем на 10, мы просто добавляем ноль в конец числа, на которое мы умножаем).
2 × 140 = 280 то же, что 2 × 14 (с нулем на конце) или 140 + 140.
Мы складываем наши ответы вместе: 1400 + 280 = 1680.
Таким образом, Джо заработал 1 680 фунтов стерлингов за четырехнедельный период.
Умножение отрицательных чисел
Умножение отрицательного числа на положительное всегда дает отрицательный ответ:
15 × (−4) = −60
Умножение отрицательного числа на другое отрицательное число всегда дает положительный ответ:
(−15) × (−4) = 60
Это полный урок с инструкциями и упражнениями для 5-го класса об умножении десятичных знаков на десятичные.Интерпретация умножения десятичной дроби на десятичную дробь состоит в том, чтобы думать об этом как о взятии дробной части десятичного числа (символ × переводится как «из»). Урок сравнивает умножение на десятичную дробь с масштабированием и сжатием палки. Наконец, он показывает общий ярлык для десятичного умножения (умножение, как если бы не было десятичных знаков; в ответе столько десятичных знаков, сколько всего множителей.) В видео ниже я объясняю правило умножения десятичных знаков (введите в ответ столько десятичных цифр, сколько в множителях.) Я объясняю, откуда взялось это правило, используя умножение дробей. Урок продолжается под видео.
1.Запишите как умножение с использованием десятичной дроби, и
решать. Помните, что «of» переводится как «×». Используйте верхнюю задачу
2. Решить. Используйте верхнюю задачу в каждом поле, чтобы помочь вам решить нижнюю.
3. Ответ. Вам не нужно рассчитывать. а. Вы узнали, что 0,1 ×
246 означает одну десятую
246. г. Кроме того, 0,1 × 0,8 означает одну десятую часть
0.8. г. Будет ли результат 1,9 × 928 больше или меньше 928?
4. Стержень усаживается . Сколько будет в пикселях? Сравните проблемы.
5. Красная палка 50 пикселей длинный. Это расширено или уменьшено .Заполнить бланки.
6.Подскажите, если полученная палка после «умножения» будет короче или длиннее оригинала.
7. Заполните рассуждения Аниты.
8. Умножьте на первое , как если бы там мы БЕЗ десятичных знаков.Затем добавьте к ответу десятичную точку.
9. Умножение.
10. Решить.
11. Найдите полную стоимость. Напишите умножение. а. Лента стоит 1,10 доллара за метр, а вы покупаете 0,4. метров. г. Стоимость орехов 8 долларов за фунт. Вы покупаете 0,3 фунта. г. Телефон звонок стоит 7 долларов в час. Говоришь 1,2 часа. г. Lace стоит 2,20 доллара за метр, и вы покупаете 1.5 метров. Здесь вы можете создать рабочие листы для десятичного умножения. Этот урок взят из книги Марии Миллер Math Mammoth Decimals 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. Он соответствует Общему базовому стандарту для 5-го класса 5.NBT.7. Math Mammoth Decimals 2 Самообучающийся рабочий текст для 5-6 классов, охватывающий четыре операции с десятичными знаками до трех десятичных знаков, с упором на десятичное умножение и деление.В книге также рассматриваются разряды, сравнение, округление, сложение и вычитание десятичных знаков. Есть много проблем с умственной математикой. Скачать (6,25 $) . Также имеется в виде печатной копии. => Узнайте больше и посмотрите бесплатные образцы! | |||
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами.Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной запятой . и они автоматически переводятся в дроби — i.е. 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей, например, 1/2: 1/3 .
Звездочка * или × — это символ умножения.
Плюс + — сложение, знак минус — — вычитание и () [] — математические скобки.
Символ возведения в степень / степени: ^ — например: (7 / 8-4 / 5) ^ 2 = (7 / 8-4 / 5) 2
Примеры:
• сложение дробей: 2 / 4 + 3/4• вычитание дробей: 2/3 — 1/2
• умножение дробей: 7/8 * 3/9
• деление дробей: 1/2: 3/4
• возведение дробей в степень: 3 / 5 ^ 3
• дробные показатели: 16 ^ 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Задачи на дроби:
следующие математические задачи »
Таблица умножения
Альтернативный формат
|
Сложение, вычитание, деление и умножение дробей
Инструкция по эксплуатации
- Введите дроби в калькулятор выше.
- Выберите математическую операцию, которую вы хотите выполнить (сложение, вычитание, умножение, деление), используя серый раскрывающийся список выбора между двумя дробями.
- Результаты будут обновляться автоматически при изменении любого значения в калькуляторе.
- Флажок под калькулятором позволяет вам выбирать между уменьшением дроби до эквивалента наименьшего общего знаменателя (если установлен) или отказом от уменьшения (если не отмечен).
Как вычислить дроби вручную
Как складывать дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.
- Сложите числители.
- Уменьшить результат до наиболее упрощенного числа.
Как вычесть дроби
- Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
- Умножьте каждый числитель на те же числа, на которые были умножены знаменатели.
- Складываем второй числитель с первого.
- Уменьшить результат до наиболее упрощенного числа.
Как умножать дроби
- Умножьте числа сверху вместе.
- Умножьте числа внизу вместе.
- Уменьшить результат до наиболее упрощенного числа.
Как разделить дроби
- Переверните вторую дробь вверх дном, чтобы получить обратное число.
- Умножьте дроби вместе (как в разделе умножения выше).
- Уменьшить результат до наиболее упрощенного числа.
Дроби: история, актуальность и популярное использование
— Руководство, составленное Корин Б. Аренас , опубликовано 22 октября 2019 г.
Практически каждый день мы имеем дело с дробями. Подумай об этом. Независимо от того, получаете ли вы четвертинки для разнообразия, покупаете одежду со скидкой 75% или готовите с половиной стакана масла, вы используете дроби.
В этом разделе мы поговорим о происхождении дробей, их важности при передаче информации и золотом сечении.
Что такое дроби?
Дроби представляют части целого числа или любое количество равных частей. Он функционирует чтобы описать, как части соотносятся с целым числом.
Для иллюстрации представьте целое число как торт. Если вы разрежете торт на 4 равные части, один кусок будет частью этого торта. В данном случае это 1/4 часть всего торта.
- 1 представляет один фрагмент или часть целого числа, которое называется числителем .
- 4 представляет, сколько всего частей содержится в целом числе, которое называется знаменателем .
Краткая история дробей
Слово Происхождение: Термин дробь происходит от латинского слово fractio что означает «сломанный». В раннем английском языке это означает «сломанный кусок или фрагмент ». Английское слово« разрушение »также имеет то же происхождение слова.
Концепция дробей существует уже более 4000 лет.Но у разных цивилизаций есть свой способ стандартизации дробей для универсального использования.
Египтяне
Согласно Математика на протяжении веков : Мягкая история для учителей и других, египтяне были одними из первых, кто придумал форму дроби еще в 1800 году до нашей эры. Их концепция в основном ограничивалась частями, иначе известными как единичные дроби. Дроби единиц используют 1 в качестве числителя.
Египетские математики создали систему с основанием 10 идея, которая похожа на системы счисления, которые мы используем сегодня.Цифра иероглифы представляли их числа, что означает символы, соответствующие определенное значение.
Поскольку числитель всегда равен 1, они должны были указать только знаменатель. Египтяне отметили знаменатель овалом или точкой над значением. Вот несколько примеров из книги Math Through the Ages :
частей были выражены как суммы долей единиц. Однако система не позволяла повторять дроби единиц в этой последовательности, что затрудняло выполнение расчетов.Чтобы решить эту проблему, египтяне создали обширные списки таблиц, в которых указаны двойные значения различных частей.
Вавилоняне
Другая цивилизация, создавшая сложную систему для По словам преподавателя математики и автора Лиз Памфри, фракции принадлежали вавилонянам.
вавилонян организовали фракции в группы по 60 человек (основание 60). Сегодня мы обычно группируем числа в группы по 10. Но для вычислений, таких как углы и минуты для времени, мы также используем основание 60.Система сгруппировала дроби по 10 и использовала два символа, один для единицы, а другой для 10.
Ниже приведены символы, представляющие вавилонскую систему счисления от 1 до 20:
.Однако у них не было символа нуля (который они позже добавили около 311 года до н.э.) или знака, который функционировал как десятичная точка для обозначения дробей целого числа. Это затрудняло интерпретацию чисел.
Например, цифры ниже читаются как 12 и 15.
По словам Памфри, символы также могут читаться как разные значения:
| x60 | шт. | Шестидесятых | Номер |
|---|---|---|---|
| 12 | 15 | ||
| 12 | 15 | 720 + 15 |
- 12 и 15 как отдельные номера
- 15/12
- 12 15/60
- 720 + 15
Как видите, отсутствие индикатора дроби делает его трудно отделить целые числа от дробей.Скорее всего, они полагались на контекст, чтобы разобраться в числовых значениях.
Как египетская, так и вавилонская системы были переданы позже людям в Греции, а затем и к средиземноморской цивилизации.
Греки
В Греции практика использования дробных величин в качестве сумм единицы дроби были довольно распространены до средневековья. Например, Liber Abbaci итальянского математика Фибоначчи — это примечательный текст 13 века. В нем широко использовались дроби, описывающие различные способы преобразования других дробей в суммы единичных дробей.
Чтобы лучше понять, ниже приводится таблица греческого языка. цифровые символы. Обратите внимание, что они такие же, как буквы в греческом алфавит:
| Значение | Квартир | Десятки | сотен |
|---|---|---|---|
| 1 | α | ι | ρ |
| 2 | β | κ | σ |
| 3 | γ | λ | τ |
| 4 | δ | µ | υ |
| 5 | ε | ν | φ |
| 6 | ϝ | ξ | χ |
| 7 | ζ | ο | ψ |
| 8 | η | π | ω |
| 9 | θ | ϙ | ϡ |
греческий запись дробей требует от читателя понимания контекста для правильного интерпретация.Чтобы выделить дробь, они ставят диакритический знак знак (‘) после знаменателя дроби.
Например, число β (2) становится ½ при записи с диакритический знак, β ’.
Аналогично, µβ (42) становится 1/42 при записи в µβ ’.
Однако здесь возникает путаница: µβ ’может также означать 40 ½. Вот почему понимание контекста имеет решающее значение при интерпретации греческих дробей.
Римлянам
У римлян дроби выражались только словами, которые усложняли любые вычисления.
Их система была основана на единице веса, называемой «as». При таком подходе 1 «as» равнялось 12 унций (римский базовая единица измерения, основа современной унции). Таким образом, дроби имеют знаменатели со значениями кратными 12.
В таблице ниже показаны римские дроби. с соответствующими условиями:
| Дробь | Римский термин |
|---|---|
| 11/12 | deunx для de uncia, забрал 1/12 |
| 10/12 | декстаны для декстанов, отнято 1/6 |
| 9/12 | dodrans for de quadrans, 1/4 отнято |
| 8/12 | bes — bi as for duae partes, 2/3 |
| 7/12 | перегородка для septem unciae |
| 6/12 | полуфабрикаты |
| 5/12 | quincunx для quinque unciae |
| 4/12 | триенс |
| 3/12 | квадрант |
| 2/12 | секстан |
| 1/12 | UNCIA |
| 1/24 | semuncia |
| 1/48 | сицилийский |
| 1/72 | скрипт |
| 1/144 | сценарий |
| 1/288 | scrupulum |
китайский
Китайцы написали Девять Главы по математическому искусству , датируемые примерно 100 годом до н. Э.С. Он включает текст о дробях, аналогичный тем, которые мы используем сегодня.
Согласно Math Through the Ages , он содержал большинство обычных правил вычисления с дробями, например, как складывать, делить и умножать дроби, а также сокращать дробь до наименьшего значения.
Однако в их системе не использовались неправильные дроби. Например, вместо неправильной дроби 9/4 они использовали бы ее эквивалентную смешанную дробь 2 1/4.
В отличие от западной математики, китайцы сосредоточились на практических приложениях, а не на теоретических рассуждениях и геометрии.
Индейцы
Индейцы разработали способ записи дробей, ближе к тому, что мы используем сегодня.
До 1000 г. до н.э. индуистские мантры в ранний ведический период вызывали силы от десяти до ста и даже до триллиона, согласно сайту The Story of Mathematics. Это свидетельство того, что ранняя индийская цивилизация использовала сложные математические операции, включая дроби, квадраты, кубы и корни.
Около 500 г. до н. Э. Они придумали систему письма, называемую брахми, которая состояла из 9 цифровых символов и нуля. Учитель математики и писатель Лиз Памфри отмечает, что эти числа во многом повлияли на современные числа, которые мы используем сегодня. См. Изображение ниже.
Индийская система записывала дроби, помещая одно значение поверх другого, точно так же, как сегодня числитель пишется над знаменателем. Однако они не поставили между ними черту. Например, дробь 4/5 будет выглядеть так:
Позже эту систему использовали арабы при торговле с индейцами.Именно арабы нарисовали черту, чтобы отличить верхнее число от нижнего числа в дроби. В конечном итоге это привело к тому, что в современную эпоху мы пишем дроби.
Как дроби улучшают способ передачи информации
По словам доктора Петерсона из MathForum.org: «дроби были изобретены, чтобы обеспечить способ работы с величинами меньше единицы».
Если люди использовали только целые числа, единственный способ сослаться на меньшие количества — использовать меньшие единицы.Это то, что сделали римляне — они использовали целые числа при измерении футов и использовали дюймы, когда им нужно было учитывать меньшие единицы.
Например, вместо 1/12 фута они будут обозначать длину как 1 дюйм, а 1/4 фута будет 3 дюйма. Но что, если вы имеете в виду 2 с половиной фута? Как насчет 1 и 3/4 фута?
Если вы выбираете стандартную длину в соответствии с футами, это сбивает с толку одновременное упоминание футов и дюймов. По сути, фракции позволяют проводить измерения без необходимости создания новые юниты.Было бы лучше учесть измерения в последовательная мода.
В США чаще используются дроби (английское измерение), поскольку для измерения при приготовлении пищи и выпечке используются чашки, а не весы.
американцев еще не приняли метрическую систему, которая является десятичная система, в которой используются единицы, относящиеся к десятичному коэффициенту. Метрическая система обычно использует граммы и литры вместо американских единиц измерения. за унции, чашки, пинты и так далее.
В таблице ниже показано преобразование объема из английской единицы измерения в ее метрический эквивалент:
Преобразование объема в метрическую систему из США
| Стандартное количество в США (на английском языке) | Метрический эквивалент | |||||
|---|---|---|---|---|---|---|
| 1 чайная ложка | 5 мл | |||||
| 1 столовая ложка | 15 мл | 9027 мл | 9027 мл 1/4 стакана или 2 жидких унции | 60 мл | ||
| 1/3 стакана | 80 мл | |||||
| 1/2 стакана или 4 жидких унции | 125 мл | |||||
| 2 / 3 стакана | 160 мл | |||||
| 3/4 стакана или 6 жидких унций | 180 мл | |||||
| 1 стакан или 8 жидких унций или 1/2 пинты | 250 мл | 02 | 1 ½ стакана или 12 жидких унций | 375 мл | ||
| 2 c ups или 1 пинта или 16 жидких унций | 500 мл | |||||
| 3 чашки или 1 ½ пинты | 700 мл | |||||
| 4 чашки или или 950 мл | ||||||
| 4 литра или 1 галлон | 3.8 л | |||||
| 1 унция | 28 граммов | |||||
| 1/4 фунта (4 унции) | 112 граммов | |||||
| 1/2 фунта (8 унций) | 225 граммов | 02 | 337 грамм | |||
| 1 фунт (16 унций) | 450 грамм |
Более того, сохранение измерений в одной единице позволяет нам складывать, вычитать, умножать и легко делить дроби.Это устраняет проблему преобразования, которая невозможна при измерении между двумя разными единицами.
Чтобы упростить вычисление дробей, воспользуйтесь калькулятором в верхней части этой страницы.
В то время как десятичные дроби предоставляют альтернативный способ обозначения дроби (и более простой способ вычисления дробей с помощью калькулятора), это необходимо понимать традиционные дроби и то, как их значения влияют на целое число.
По данным Thoughtco.com, студенты, которые не осваивают дроби в ранние годы, имеют тенденцию запутаться и испытать математическое беспокойство.Они также упомянули половину американской восьмерки. грейдеры не могут расположить дроби по значению.
Интуитивное обучение дробям помогает детям развить более широкое понимание теоретических математических концепций, позволяя им использовать их в реальной жизни. Это намного лучше, чем запоминать таблицы с единицами измерения или символами.
Золотое сечение и последовательность Фибоначчи
В математике соотношение — это, по сути, сравнение двух числа, которые зависят от типа сравниваемых чисел.
Вы можете встретить такой пример: 1: 3 или 1 из 3. Например, бутылка концентрата апельсинового сока состоит из 1 части апельсина. сок и 3 части воды. Это также можно записать в виде дроби, 1/3.
Коэффициенты относятся к дробям, потому что они сравнивают разные ценности, которые могут представлять собой целое. В этом примере бутылка целиком апельсинового сока.
Золотое сечение — специальное число, представленное греческим символом фи ( φ ) с приблизительным значением 1.618.
Получается путем разделения линии на 2 части, так что длинный отрезок (а) деленная на короткую часть (б) равна всей длине, разделенной на длинный раздел.
Чтобы лучше понять, вот иллюстрация со стандартным уравнением:
Исторически сложилось так, что соотношение соблюдалось в древних такие сооружения, как Парфенон и пирамиды Египта. В Великой пирамиде Гизы отношение основания к высоте примерно 1.5717, что является близко к золотому сечению. Он также встречается в повторяющихся закономерностях в природе, таких как как лепестки цветов, ракушки, ветви деревьев и спиральные галактики.
С другой стороны, Фибоначчи последовательность — еще одна известная математическая формула. Последовательность получена из сумма двух предшествующих чисел. Многие источники говорят, что Леонардо Фибоначчи (Леонардо Пизанский) популяризировал его в своей книге Liber Abacci .
Но согласно Live Science, математик Кейт Девлин, автор книги Finding Fibonacci: The Quest to «Откройте для себя заново забытого математического гения, изменившего мир, », — говорится в сообщении. что Леонардо Фибоначчи на самом деле не «открыл» последовательность.
Древние санскритские сочинения, в которых использовались индуистско-арабские цифры системы были первыми, кто обсудил это за столетия до Леонардо Фибоначчи.
Последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811 и так далее…
Когда математики создают квадраты на основе этой последовательности, они могут нарисовать спираль.
Как золотое сечение связано с последовательностью Фибоначчи?
Исследователи заметили, что когда вы берете любые два последовательных числа Фибоначчи, их отношение очень близко к золотому сечению.Таким образом, φ составляет примерно 1,618. Чтобы дать вам представление, см. Таблицу ниже.
| A | B | B / A | |||
|---|---|---|---|---|---|
| 2 | 3 | 1,5 | |||
| 3 | 5 | 1,66626627 | 9027 9027 9027 | ||
| 8 | 13 | 1,625 |
Итоги
Понятие дроби было разработано разными древними цивилизациями.Одними из первых, кто изобрели дробную систему с обширными таблицами, были египтяне. Другие древние общества, такие как вавилоняне, греки, римляне и китайцы, также внесли свой вклад в его улучшение. Но на современные цифры и то, как мы пишем дроби, в основном повлияли индейцы, которые ввели индуистско-арабскую систему счисления.
Использование дробей помогает нам легко передавать информацию об измерениях. Это не позволяет людям использовать разные единицы измерения, что упрощает их расчет.
Наконец, дроби связаны со знаменитым золотым рационом и последовательностью Фибоначчи, которая во многом повлияла на то, как мы проектируем все виды структур.
Об авторе
Корин — страстный исследователь и автор финансовых тем, изучающий экономические тенденции, их влияние на население, а также то, как помочь потребителям принимать более мудрые финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма в Филиппинском университете, одном из ведущих учебных заведений в мире, и степень бакалавра коммуникационных искусств в колледже Мириам.
 Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.
Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.