Парные и непарные согласные звуки
В русском языке согласные звуки делятся на твердые и мягкие, звонкие и глухие. В каждом случае есть согласные, у которых есть пара, а также согласные, у которых пары нет. Давайте рассмотрим парные и непарные согласные, и в каких словах они встречаются.
Итак, рассмотрим гласные звуки, которые делятся на твердые и мягкие. Чтобы на письме обозначить мягкий гласный звук ставится символ (‘).
По твёрдости-мягкости большинство звуков образуют пары:
[б] – [б’] (быть – бить),
[п] – [п’] (пыль – пил),
[в] – [в’] (выл – вил),
[ф] – [ф’] (готов – готовь),
[д] – [д’] (воды– води),
[т] – [т’] (бит – бить),
[з] – [з’] (везу – вези),
[с] – [с’] (вес – весь),
[л] – [л’] (мол – моль),
[н] – [н’] (кон –конь),
[р] – [р’] (рысь – рис),
[к] – [к’] (сорока – сороки),
[г] – [г’] (нога – ноги),
[х] – [х’] (уха – ухи).
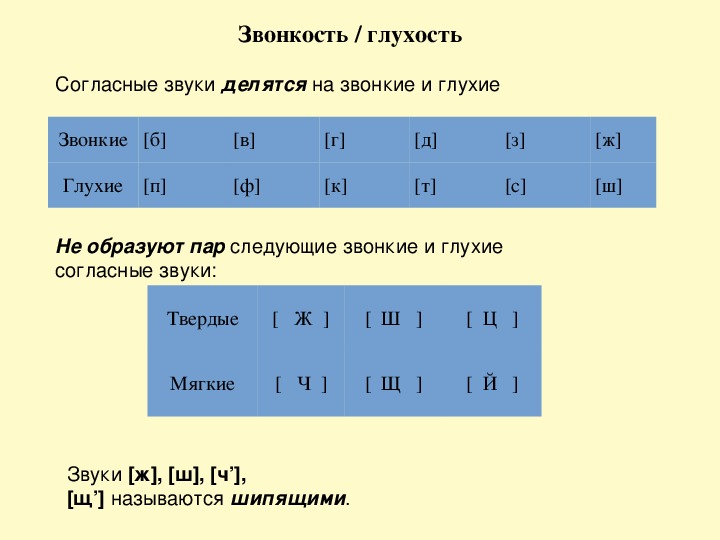
К твердым непарным относят согласные [ц], [ш], [ж], а к мягким непарным – согласные [ч’], [щ’], [й’]
Теперь, давайте рассмотрим разделение гласных звуков на звонкие и глухие.
Согласные звуки, образующиеся при участии голоса, называются звонкими: [б], [в], [г], [д], [ж], [з], [л], [м], [н], [р].
Согласные звуки, образующиеся без участия голоса, называются глухими: [к], [п], [с], [т], [ф], [х], [ц], [ч], [ш], [щ].
Звонкие и глухие согласные образуют соотносительные пары: [б] – [п], [г] – [к], [д] – [т], [з] – [с], [в] — [ф], [ж] — [ш], [г’] — [к’], [б’] — [п’], [в’] — [ф’], [з’] — [с’], [д’] — [т’].
Звуки [л], [м], [н], [р] всегда звонкие, они не имеют соответствующих глухих звуков.
Звуки [х], [ц], [ч] всегда глухие.
Мы с вами рассмотрели просто классификацию согласных звуков в русском языке. Знание данной классификации позволит нам в дальнейшем понимать правила грамматики языка.
Непарные согласные звуки звонкие и глухие, твердые и мягкие
Непарные согласные — это звуки, которые не соотносятся с другими согласными по признаку звонкости/глухости или твёрдости/мягкости.
Выясним, какие непарные согласные звуки существуют в русском языке и какие фонетические особенности они имеют.
Звонкие и глухие согласные
Чтобы понять, что такое непарные согласные, вначале определим, что наша речь состоит из предложений, предложения — из слов, а слова — из звуков.
Звук — это минимальная единица речи, которая сама по себе не имеет значения, но объединившись с другими звуками создает фонетический облик слова, имеющего лексическое значение.
Звуки речи произносятся по-разному. Если струя воздуха проходит свободно через напряжённые голосовые связки и полость рта, то образуются гласные звуки [а], [о], [э], [у], [и], [ы]. Гласные звуки формируются целиком голосом.
Большинство звуков речи образуются, когда выдыхаемый воздух встречает препятствия в виде языка, зубов, смыкания и размыкания губ и пр. Тогда появляется шумный звук, который называется согласным.
По соотношению голоса и шума согласные звуки делятся на звонкие и глухие.
Звонкие согласные состоят из шума и голоса:
[б], [в], [г], [д], [ж], [з]
А глухие согласные, напротив, «безголосые». Они состоят только из шума:
[к], [п], [с], [т], [ф], [х], [ц], [ч’], [ш], [щ’]
Многие звонкие и глухие согласные похожи по способу образования, но различаются только своей звонкостью, то есть участием голоса, или глухостью. По признаку звонкости/глухости такие согласные составляют пары:
- [б] — [п]
- [в] — [ф]
- [г]- [к]
- [д] — [т]
- [ж] — [ш]
- [з] — [с].
Это парные согласные, которые различаются признаком звонкости/глухости.
В фонетике русского языка существует 6 пар звонких и глухих согласных. С их помощью можно различать слова:
- убор — упор;
- влага — фляга;
- грот — крот;
- дрова — трава:
- жалость — шалость;
- зев — сев.

Остальные согласные являются непарными.
Непарные звонкие согласные
В русском языке существуют непарные согласные, в образовании которых голоса больше, чем шума. При их образовании воздух проходит через гортань и голосовые связки напрягаются и вибрируют, то есть в их рождении участвует голос.
Эти звуки отличаются от звонких согласных своей особой звучностью, поэтому их назвали сонорными. Это название восходит к латинскому слову sonorus, что значит «звучный».
В формировании сонорных звуков шум тоже присутствует, но в меньшей степени, чем у звонких согласных.
Например, воздух проходит через нос и образует звуки [н] и [н’], а при смыкании губ получаются звуки [м] и [м’].
Если воздух встречает препятствие в виде языка и проходит в проход между краями щёк, то появляются звуки [л] и [л’].
Кончик языка поднимается к альвеолам и дрожит под выходящей струей воздуха. Тогда рождаются звуки [р] и [р’].
Тогда рождаются звуки [р] и [р’].
Если растянуть губы в улыбке, а кончик языка прижать к нижним зубам, то произнесем звук [й’].
Эти всегда звонкие звуки, которые произносятся с участием голоса и шума, не соотносятся ни с какими глухими согласными. У них нет фонетической пары по признаку глухости/звонкости.
Определение
Звуки [й], [л], [л’], [м], [м’], [н], [н’], [р], [р’] — это непарные согласные.
Между собой они образуют пары по признаку твёрдости/мягкости:
- [л] — [л’]
- [м] — [м’]
- [н] — [н’]
- [р] — [р’]
Послушаем, как звучат мягкие и твердые сонорные звуки в словах:
- банка — банька;
- рад — ряд;
- мыс — миска;
- лов — лев.
А звук [й’] непарный по всем характеристикам:
- непарный звонкий;
- непарный мягкий.
Непарные глухие согласные
Среди глухих согласных также есть непарные, которые не соотносятся со звонкими согласными.
Определение
Звуки [х], [х’], [ц], [ч’], [щ’] — это непарные глухие согласные.
Глухие согласные [х] и [х’] образуют пару по признаку твёрдости/мягкости:
- храбрый — хитрый;
- хлеб — химия;
- худой — хилый.
Остальные глухие согласные непарные по всем фонетическим признакам. Укажем их особенности:
- звук [ц] — это непарный глухой, непарный твердый;
- звук [ч’] — это непарный глухой, непарный мягкий;
- звук [щ’] — это непарный глухой, непарный мягкий.
Непарные мягкие и твёрдые согласные
Вне зависимости от последующего гласного, обозначенного буквами «е», «ё», «и», «ю», «я», или «ь», звуки [ц], [ж], [ш] всегда твердые в словах, а [й’], [ч’ ] и [щ’], напротив, звучат мягко. B транскрипции слов их мягкость всегда обозначается апострофом.
Сравним:
- ци́ркуль [ц ы р к ул’]
- це́нный [ц э н: ы й’]
- жёлтый [ж о л т ы й’]
- за́лежь [з а л’ и ж]
- кошёлка [к а ш о л к а]
- пу́стошь [п у с т а ш]
- чёрный [ч’ о р н ы й’]
- чистота́ [ч’ и с т а т а]
- щётка [щ’ о т к а]
- щу́ка [щ’ у к а].

Мягкий знак после шипящих согласных, обозначенных буквами «ж», «ш», «ч», «щ» служит для обозначения существительных женского рода (залежь, пустошь, вещь, речь) или форм глаголов (беречь, поёшь, отрежь), а не для указания мягкости согласного.
Итак, в фонетике русского языка три согласных [й’] [ч’] [щ’] являются непарными мягкими, а звуки [ж], [ш], [ц] — непарными твёрдыми.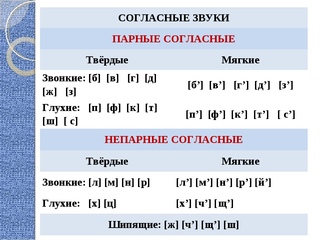
Парный твердый звонкий глухой. Парные и непарные согласные
Одни согласные звуки в русском языке называются глухими, так как они состоят из одного шума, т.е. образуются без участия голоса. Таких согласных десять: к, п, с, т, ф, х, ц, ч, ш, щ.

Среди звонких согласных выделяются особо звучные, в которых голос явно преобладает над шумом. Таких согласных четыре: л, м, н, р. Они называются сонорными.
Звуки ж, ч, ш, щ называются еще шипящими.
Звонкие согласные б, в, г, д, ж, з имеют парные глухие п, ф, к, т, ш, с. Остальные соответствующих пар не имеют (см. таблицу).
Глухие согласные: п, ф, к, т, с, ш
Звонкие согласные б, в, г, д, ж, з на конце слова или в середине слова перед глухим согласным оглушаются. Например: столбы — столб (п), тазы — таз (с), годы — год (т), дружок — дружка (ш), ловок — ловкий (ф), скользить — скользкий (с) и т. д.
Звонкие сонорные согласные л, м, н, р не оглушаются.
Глухие согласные звуки к, п, с, т, ф, ш озвончаются перед звонкими согласными. Например: сбор (з),.молотьба (д).
Озвончение и оглушение согласных, как правило, при написании не обозначается.
Упражнение 56. Укажите количество звуков в приводимых ниже словах и назовите каждый из них.

Мозг, работа, стол, народ, вьюн, яма, дрожжи, учение, массаж, мой, веять.
Упражнение 57. Объясните, чем различается произношение и написание приводимых ниже слов.
Сделать, труд, просьба, сладкий, пробка, подходить, подбивать, ялик, отъезд, дрозд, даем.
Упражнение 58. Укажите случаи озвончения и оглушения согласных.
Горб, съезд, сделать, отбить, резкий, сжать, редкий, везти, дуб, косьба, низкий.
Упражнение 59. Спишите, вставляя пропущенные буквы, и укажите, какому звуку соответствует каждая из вставленных букв.
Ра.amp;шить, разбить, о.Гбежать, раЗ.дать, раС.чет, объamp;м.
Упражнение 60. Спишите предложение, подчеркивая согласные, обозначающие звуки, которые имеют пары по звонкости — глухости.
Еще по теме § 21. Согласные глухие и звонкие:
- § 3. ПРАВОПИСАНИЕ СОГЛАСНЫХ (проверяемые и непроверяемые, звонкие, глухие и непроизносимые согласные; двойные согласные; сочетания согласных)
Современный русский алфавит состоит из 33 букв. Фонетика современного русского числа определяет 42 звука. Звуки бывают гласные и согласные. Буквы ь (мягкий знак) и ъ (твёрдый знак) не образуют звуков.
Фонетика современного русского числа определяет 42 звука. Звуки бывают гласные и согласные. Буквы ь (мягкий знак) и ъ (твёрдый знак) не образуют звуков.
Гласные звуки
В русском языке 10 гласных букв и 6 гласных звуков.
- Гласные буквы: а, и, е, ё, о, у, ы, э, ю, я.
- Гласные звуки: [а], [о], [у], [э], [и], [ы].
Для запоминания гласные буквы часто записывают парами по сходному звучанию: а-я, о-ё, е-э, и-ы, у-ю.
Ударные и безударные
Число слогов в слове равно числу гласных в слове: лес — 1 слог, вода — 2 слога, дорога — 3 слога и т.д. Слог, который произносится с большей интонацией, является ударным. Гласная, образующая такой слог, является ударной, остальные гласные в слове — безударными. Положение под ударением называют сильной позицией, без ударения — слабой позицией.
Йотированные гласные
Значимое место занимают йотированные гласные — буквы е, ё, ю, я, которые означают два звука: е → [й’][е], ё → [й’][о], ю → [й’][у], я → [й’][а].
- стоят в начале слова (ель, ёлка, юла, якорь),
- стоят после гласного (какое, поёт, заяц, каюта),
- стоят после ь или ъ (ручье, ручьём, ручью, ручья).
В остальных случаях буквы е, ё, ю, я означают один звук, но однозначного соответствия нет, так как различные позиции в слове и различные сочетания с согласными этих букв рождают разные звуки.
Согласные звуки
Всего 21 согласная буква и 36 согласных звуков. Несоответствие в количестве означает, что некоторые буквы могут означать разные звуки в разных словах — мягкие и твёрдые звуки.
Согласные буквы: б, в, г, д, ж, з, й, к, л, м, н, п, р, с, т, ф, х, ц, ч, ш, щ.
Согласные звуки: [б], [б’], [в], [в’], [г], [г’], [д], [д’], [ж], [з], [з’], [й’], [к], [к’], [л], [л’], [м], [м’], [н], [н’], [п], [п’], [р], [р’], [с], [с’], [т], [т’], [ф], [ф’], [х], [х’], [ц], [ч’], [ш], [щ’].
Знак ‘ означает мягкий звук, то есть буква произносится мягко. Отсутствие знака говорит о том, что звук твёрдый. Так, [б] — твёрдый, [б’] — мягкий.
Отсутствие знака говорит о том, что звук твёрдый. Так, [б] — твёрдый, [б’] — мягкий.
Звонкие и глухие согласные
По тому, как мы произносим согласные звуки, существует разница. Звонкие согласные — образуются в сочетании голоса и шума, глухие согласные — образуются за счёт шума (голосовые связки не вибрируют). Всего 20 звонких согласных звуков и 16 глухих согласных звуков.
| Звонкие согласные | Глухие согласные | ||
|---|---|---|---|
| непарные | парные | парные | непарные |
| й → [й»] | б → [б], [б»] | п → [п], [п»] | ч → [ч»] |
| л → [л], [л»] | в → [в], [в»] | ф → [ф], [ф»] | щ → [щ»] |
| м → [м], [м»] | г → [г], [г»] | к → [к], [к»] | ц → [ц] |
| н → [н], [н»] | д → [д], [д»] | т → [т], [т»] | |
| р → [р], [р»] | ж → [ж] | ш → [ш] | |
| з → [з], [з»] | с → [с], [с»] | ||
| 9 непарных | 11 парных | 11 парных | 5 непарных |
| 20 звонких звуков | 16 глухих звуков | ||
По парности-непарности звонкие и глухие согласные делятся на:
б-п, в-ф, г-к, д-т, ж-ш, з-с
— парные по звонкости-глухости.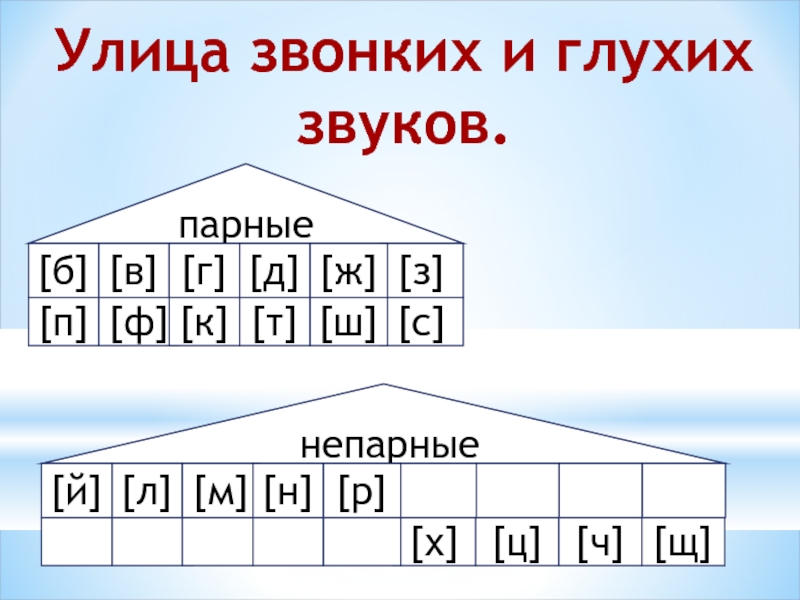
й, л, м, н, р
— всегда звонкие (непарные).
x, ц, ч, щ
— всегда глухие (непарные).
Непарные звонкие согласные называются сонорными.
Среди согласных по уровню «шумности» также выделяют группы:
ж, ш, ч, щ
— шипящие.
б, в, г, д, ж, з, к, п, с, т, ф, х, ц, ч, ш, щ
— шумные.
Твёрдые и мягкие согласные
| Твёрдые согласные | Мягкие согласные | ||
|---|---|---|---|
| непарные | парные | парные | непарные |
| [ж] | [б] | [б»] | [ч»] |
| [ш] | [в] | [в»] | [щ»] |
| [ц] | [г] | [г»] | [й»] |
| [д] | [д»] | ||
| [з] | [з»] | ||
| [к] | [к»] | ||
| [л] | [л»] | ||
| [м] | [м»] | ||
| [н] | [н»] | ||
| [п] | [п»] | ||
| [р] | [р»] | ||
| [с] | [с»] | ||
| [т] | [т»] | ||
| [ф] | [ф»] | ||
| [х] | [х»] | ||
| 3 непарных | 15 парных | 15 непарных | 3 парных |
| 18 твёрдых звуков | 18 мягких звуков | ||
Глухие согласные
Согласные звуки, образуемые при помощи одного шума, без участия голоса: (к), (к’), (п), (п’), (с), (с’), (т), (т’), (ф), (ф’1, (х), (х’), (ц), (ч), (ш), (ш’) (щ).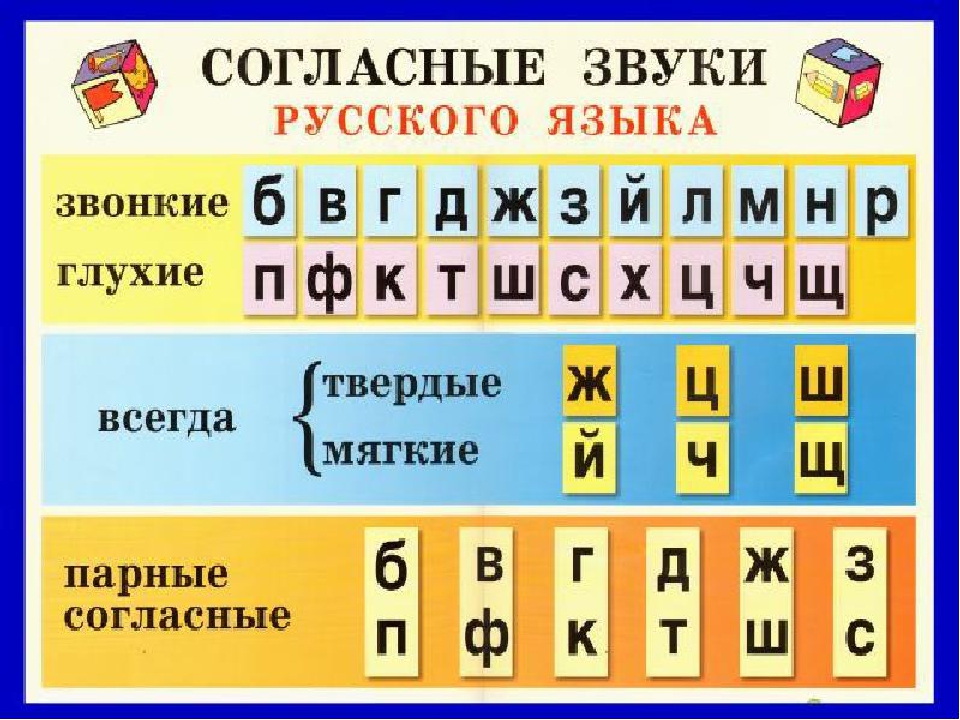
Словарь-справочник лингвистических терминов. Изд. 2-е. — М.: Просвещение . Розенталь Д. Э., Теленкова М. А. . 1976 .
Смотреть что такое «глухие согласные» в других словарях:
ГЛУХИЕ СОГЛАСНЫЕ. Звуки, состоящие акустически из одного шума, производимого органами речи (см. Шумные согласные), без участия голоса; голосовые связки приэтом или раскрыты или, хотя и сближены, но не натянуты, отчего выдыхаемый воздух, проходя… … Литературная энциклопедия
Глухие согласные — ГЛУХИЕ СОГЛАСНЫЕ. Звуки, состоящие акустически из одного шума, производимого органами речи (см. Шумные согласные), без участия голоса; голосовые связки приэтом или раскрыты или, хотя и сближены, но не натянуты, отчего выдыхаемый воздух,… … Словарь литературных терминов
Основная статья: Согласные Глухие согласные тип согласных, произносимых без вибрации гортани. Глухота тип фонации, наряду с звонкостью и состоянием гортани. В Международном фонетическом алфавите имеются различные буквы для звонких и глухих… … Википедия
Согласные, произносимые без участия голоса, т. е. при раздвинутых и ненапряжённых голосовых связках, например русские «п», «т», «к», «ф», «с». См. Согласные …
е. при раздвинутых и ненапряжённых голосовых связках, например русские «п», «т», «к», «ф», «с». См. Согласные …
глухие согласные — Звуки, состоящие акустически из одного шума, производимого органами речи (см. шумные согласные), без участия голоса; голосовые связки приэтом или раскрыты или, хотя и сближены, но не натянуты, отчего выдыхаемый воздух, проходя через них,… … Грамматический словарь: Грамматические и лингвистические термины
Звонкие и глухие согласные
Звонкие и глухие согласные — 1. Для проверки написания сомнительной согласной нужно изменить форму слова или подобрать родственное слово, с тем чтобы за проверяемым согласным стоял гласный звук или один из согласных л, м, н, р. Например: смазка – смазать, молотьба –… … Справочник по правописанию и стилистике
Согласные — Согласные класс звуков речи, противоположных по своим свойствам гласным. Артикуляционные свойства согласных: обязательное наличие преграды в речевом тракте; с акустической точки зрения согласные характеризуются как звуки, при образовании которых … Лингвистический энциклопедический словарь
Запрос «Согласный» перенаправляется сюда; см. также другие значения. Согласные звуки речи, сочетающиеся в слоге с гласными и в противоположность им не образующие вершины слога. Акустически согласные обладают относительно меньшей, чем гласные,… … Википедия
также другие значения. Согласные звуки речи, сочетающиеся в слоге с гласными и в противоположность им не образующие вершины слога. Акустически согласные обладают относительно меньшей, чем гласные,… … Википедия
Звуки речи, сочетающиеся в слоге с гласными и в противоположность им не образующие вершины слога. Акустически С. обладают относительно меньшей, чем гласные, общей энергией и могут не иметь четкой формантной (см. Форманта) структуры.… … Большая советская энциклопедия
Книги
- Глухие согласные , Варламов Игорь Валерьевич. Москва и Магнитогорск — два города, определивших творческую судьбу Игори Варламова. О литературно-художественной среде двух городов, в каждом из которых был свой официоз и своя контркультура,…
Многие русские согласные образуют пары по твердости-мягкости: – , – и другие. Звуки, соответствующие ударным и, после мягких согласных в слабой, безударной позиции звучат одинаково. Буква обозначает звук, например гласные после твёрдых согласных и согласные перед гласными: погода.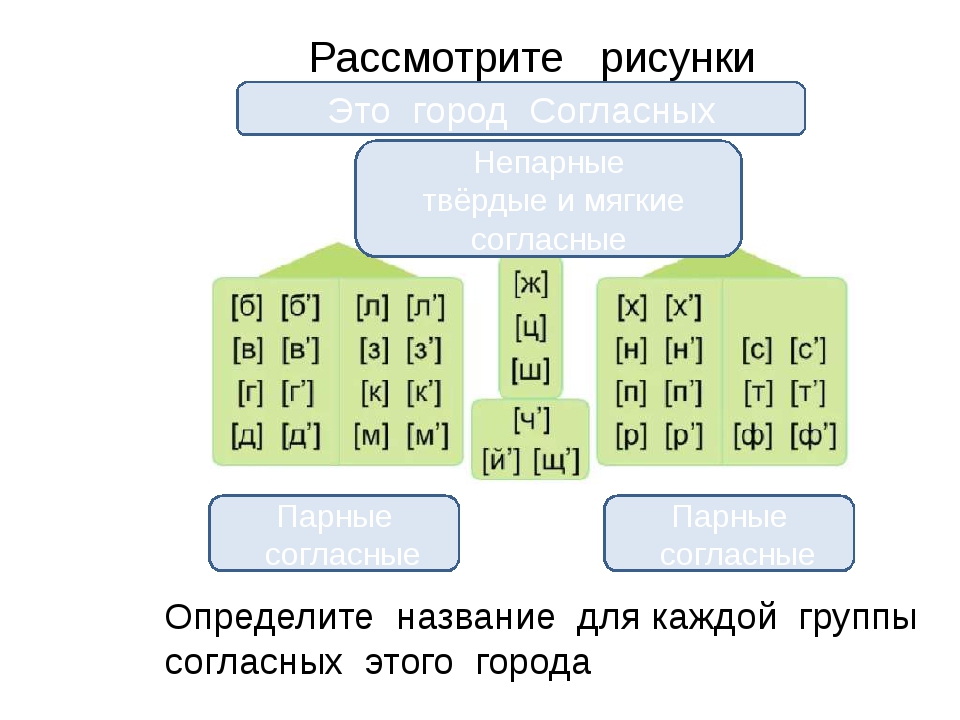
Ведущая Василиса попросила повторить всё, что выучили ученики про согласные. Друзья из Шишкиного Леса вспомнили немало: Согласных больше чем гласных. Согласные нельзя спеть. Они произносятся с шумом и голосом: Б, Ж, З. Или только с шумом: П, Т, Ф. Согласные бывают звонкие глухие парные непарные.
§6. Твёрдые и мягкие согласные
Всё дело в том, что ты пропустил предыдущий урок, на котором мы изучали парные согласные, — пояснила Василиса. Звонкому «Ж» парным будет глухой «Ш». Например: жар — шар. — Я понял, – сказал Зубок. Глухой звук это то же что и звонкий, но сказанный тихо, без голоса. Достаточно изменить слово так, чтобы после непонятного согласного стояла гласная. Однако не все согласные парные.
В одном будут жить парные согласные, а в другом — непарные. Парные Непарные Ж — Ш М, Н З — С Х, Ц К — Г Р, Л А теперь давайте составим рассказ из слов, в которых только непарные согласные. Хоть и парные эти согласные, Но они всё равно очень разные. В безударной позиции гласные произносятся менее четко и звучат с меньшей длительностью (т. е. редуцируются).
е. редуцируются).
Сколько пар образуют согласные по глухости-звонкости?
Не забывайте, что парные звонкие согласные в слабой позиции на конце слова или перед глухим согласным всегда оглушаются, а глухие перед звонким – иногда озвончаются. Когда буквы, обыкновенно обозначающие глухие согласные, при озвончении обозначают звонкие звуки, это кажется настолько необычным, что может привести к ошибкам в транскрипции. В заданиях, связанных со сравнением количества букв и звуков в слове, могут быть «ловушки», провоцирующие ошибки.
Возможны слова, которые могут состоять только из гласных, но согласные тоже необходимы. В русском языке согласных намного больше, чем гласных. Согласные – это звуки, при произнесении которых воздух встречает на своём пути преграду. В русском языке два вида преграды: щель и смычка – это два основных способа образования согласных.
Смычка, второй вид артикуляции согласных,образуется при смыкании органов речи. Поток воздуха резко преодолевает эту преграду, звуки получаются краткими, энергичными. Сравним слова: дом и кот. В каждом слове по 1-му гласному звуку и по 2 согласных.
Сравним слова: дом и кот. В каждом слове по 1-му гласному звуку и по 2 согласных.
2) перед ними не происходит озвончение парных глухих согласных (т.е. позиция перед ними сильная по глухости-звонкости, как и перед гласными). Но есть звуки, у которых нет пары по признаку твёрдости-мягкости. В школьных учебниках сказано, что и — непарные по твёрдости-мягкости. Как же так? Мы ведь слышим, что звук – это мягкий аналог звука.Когда в школе училась я сама, я не могла понять почему?
Парные по звонкости-глухости согласные звуки
Недоумение возникает, потому что школьные учебники не учитывают, что звук ещё и долгий, а твёрдый нет. Пары – это звуки, различающиеся только одним признаком. А и – двумя. Поэтому и не являются парами. Во-первых, ребята поначалу часто смешивают звуки и буквы. Использование буквы в транскрипции создаст основание для такого смешения, спровоцирует ошибку.
Нужно понять, осмыслить, а потом запомнить, что на самом деле звуки и пару по твёрдости-мягкости не образуют. Важны условия, в которых оказывается тот или иной звук. Начало слова, конец слова, ударный слог, безударный слог, положение перед гласным, положение перед согласным – всё это разные позиции.
Важны условия, в которых оказывается тот или иной звук. Начало слова, конец слова, ударный слог, безударный слог, положение перед гласным, положение перед согласным – всё это разные позиции.
В безударных слогах гласные подвергаются изменениям: они короче и не произносятся так же отчётливо, как под ударением. И под ударением, и в безударной позиции мы ясно слышим: , и пишем буквы, которыми эти звуки принято обозначать. Упростили. Но многие ребята с хорошим слухом, слышащие ясно, что звуки в следующих примерах разные, никак не могут понять, почему учитель и учебник настаивают на том, что эти звуки одинаковы.
В ней наблюдается прояснение гласных после мягких согласных. Позиционные изменения наблюдаются только у парных согласных. Во всех случаях в слабой позиции возможно позиционное смягчение согласных. Естественно, в школьной традиции не принято излагать характеристики звуков и происходящих с ними позиционных изменений со всеми подробностями. Поэтому ниже представлен список позиционно-обусловленных изменений согласных по признакам способа и места образования.
Буква может обозначать качество предшествующего звука, например ь в словах тень, пень, пальба. Сравнение с гласными звуками. Каждый согласный имеет признаки, отличающие его от остальных согласных звуков. В речи может происходить замена звуков под влиянием соседних звуков в слове. Важно знать сильные и слабые позиции согласных звуков в слове для их правильного написания.
Классификация согласных.
Если человек произносит согласные звуки, то закрывает (хоть немного) рот, из-за этого получается шум. Но шумят согласные по-разному. Заселим фонетические домики в городе звуков. Договоримся: на первом этаже будут жить глухие звуки, а на втором – звонкие.
У звуков и нет парных мягких звуков, они всегда твёрдые. Но не все согласные звуки и буквы образуют пары. Те согласные, которые пар не имеют, называют непарные. Поселим непарные согласные звуки в свои домики. Звуки второго домика называют ещё сонорными, потому что образуются они с помощью голоса и почти без шума, они очень звучные. В первую положим те, в названиях которых слышно какие-либо мягкие звуки, во вторую те, в названиях которых все согласные звуки твёрдые.
В первую положим те, в названиях которых слышно какие-либо мягкие звуки, во вторую те, в названиях которых все согласные звуки твёрдые.
Чтобы не перепутать при прочтении транскрипции твёрдые и мягкие звуки, учёные договорились показывать мягкость звука значком, очень похожим на запятую, только ставят его сверху.
И тогда мы поймём точно — какую букву нужно писать. Давайте вместе найдём в русской азбуке этих одиночек. Он этого не заметил, потому что смотрел на луну. И тут вошёл его верный рыцарь. И спугнул муху. Молодцы! То ли звонкий, то ли потише, Кот — кота, год — года. Различим без труда. И в конец букву верно напишем. Гласные, без ударения в целом сохраняют свое звучание. Буквы е, ё, ю, я играют двойную роль в русской графике. Звук – минимальная единица звучащей речи. У каждого слова есть звуковая оболочка, состоящая из звуков.
Звуки делятся на гласные и согласные.У них разная природа. По соотношению шума и голоса согласные делятся на звонкие и глухие. Нормативным произношением считается «иканье», т. е. неразличение Э и А в безударном положении после мягких согласных. Такое изменение гласных в слабой позиции называется редукцией. В слове гласные могут быть в ударных и безударных слогах. В слабых позициях согласные видоизменяются: с ними происходят позиционные изменения.
е. неразличение Э и А в безударном положении после мягких согласных. Такое изменение гласных в слабой позиции называется редукцией. В слове гласные могут быть в ударных и безударных слогах. В слабых позициях согласные видоизменяются: с ними происходят позиционные изменения.
В русском языке 21 согласная буква и 36 согласных звуков. Согласные буквы и соответствующие им согласные звуки:
б — [б], в — [в], г — [г], д — [д], ж — [ж], й — [й], з — [з], к — [к], л — [л], м — [м], н — [н], п — [п], р — [р], с — [с], т — [т], ф — [ф], х — [х], ц — [ц], ч — [ч], ш — [ш], щ — [щ].
Согласные звуки делятся на звонкие и глухие, твёрдые и мягкие. Они бывают парные и непарные. Всего 36 различных комбинаций согласных по парности-непарности твёрдых и мягких, глухих и звонких: глухих — 16 (8 мягких и 8 твёрдых), звонких — 20 (10 мягких и 10 твёрдых).
Схема 1. Согласные буквы и согласные звуки русского языка.
Твёрдые и мягкие согласные звуки
Согласные бывают твёрдыми и мягкими. Они делятся на парные и непарные. Парные твёрдые и парные мягкие согласные помогают нам различать слова. Сравните: конь [кон’] — кон [кон], лук [лук] — люк [л’ук].
Они делятся на парные и непарные. Парные твёрдые и парные мягкие согласные помогают нам различать слова. Сравните: конь [кон’] — кон [кон], лук [лук] — люк [л’ук].
Для понимания объясним «на пальцах». Если согласная буква в разных словах означает либо мягкий, либо твёрдый звук, то звук относится к парным. Например, в слове кот буква к обозначает твёрдый звук [к], в слове кит буква к обозначает мягкий звук [к’]. Получаем: [к]-[к’] образуют пару по твёрдости-мягкости. Нельзя относить к паре звуки для разных согласных, например [в] и [к’] не составляют пару по твёрдости-мягкости, но составляет пара [в]-[в’]. Если согласный звук всегда твёрдый либо всегда мягкий, то он относится к непарным согласным. Например, звук [ж] всегда твёрдый. В русском языке нет слов, где бы он был мягким [ж’]. Так как не бывает пары [ж]-[ж’], то он относится к непарным.
Звонкие и глухие согласные звуки
Согласные звуки бывают звонкие и глухие. Благодаря звонким и глухим согласным мы различаем слова. Сравните: шар — жар, кол — гол, дом — том. Глухие согласные произносятся почти с прикрытым ртом, при их произнесении голосовые связки не работают. Для звонких согласных нужно больше воздуха, работают голосовые связки.
Сравните: шар — жар, кол — гол, дом — том. Глухие согласные произносятся почти с прикрытым ртом, при их произнесении голосовые связки не работают. Для звонких согласных нужно больше воздуха, работают голосовые связки.
Некоторые согласные звуки имеют схожее звучание по способу произношения, но произносятся с разной тональностью — глухо или звонко. Такие звуки объединяются в пары и образуют группу парных согласных. Соответственно, парные согласные — это пара из глухой и звонкой согласной.
- парные согласные: б-п, в-ф, г-к, д-т, з-с, ж-ш.
- непарные согласные: л, м, н, р, й, ц, х, ч, щ.
Сонорные, шумные и шипящие согласные
Сонорные — звонкие непарные согласные звуки. Сонорных звуков 9: [й’], [л], [л’], [м], [м’], [н], [н’], [р], [р’].
Шумные согласные звуки бывают звонкие и глухие:
- Шумные глухие согласные звуки (16): [к], [к»], [п], [п»], [с], [с»], [т], [т»], [ф], [ф»], [х], [х’], [ц], [ч’], [ш], [щ’];
- Шумные звонкие согласные звуки (11): [б], [б’], [в], [в’], [г], [г’], [д], [д’], [ж], [з], [з’].

Шипящие согласные звуки (4): [ж], [ч’], [ш], [щ’].
Парные и непарные согласные звуки
Согласные звуки (мягкие и твёрдые, глухие и звонкие) делятся на парные и непарные. Выше в таблицах показано деление. Обобщим всё схемой:
Схема 2. Парные и непарные согласные звуки.
Чтобы уметь делать фонетический разбор, помимо согласных звуков нужно знать
Глухие и звонкие согласные / Согласные звуки и буквы, их обозначающие / Звуки и буквы / Справочник по русскому языку для начальной школы
- Главная
- Справочники
- Справочник по русскому языку для начальной школы
- Звуки и буквы
- Согласные звуки и буквы, их обозначающие
- Глухие и звонкие согласные
Согласные звуки могут произноситься с большей или меньшей степенью звучности. В соответствии с этим выделяют звонкие и глухие согласные.
Глухие согласные звуки состоят из шума, а звонкие согласные звуки — из шума и голоса.
Некоторые согласные звуки являются парными по звонкости-глухости, т.е. могут озвончаться или оглушаться в зависимости от положения в слове. А некоторые являются непарными, т.е. их звучание не зависит от положения.
Таблица согласных звуков парных и непарных по звонкости/глухости:
Группы согласных | Парные | Непарные |
| Звонкие | [б], [б’], [в], [в’], [г], [г’], [д], [д’], [ж], [з], [з’] | [й’], [р], [р’], [л], [л’], [м], [м’], [н], [н’] |
| Глухие | [п], [п’], [ф], [ф’], [к], [к’], [т], [т’], [ш], [с], [с’] | [ц], [х], [х’], [ч’], [щ’] |
Согласные парные звонкие звуки оглушаются:
- в конце слова — зуб [зуп], стог [сток], плов [плоф]
- перед глухими согласными звуками — губки [гупки], ложка [лошка], низко [н’иска]
Согласные парные глухие звуки озвончаются:
- перед звонкими согласными звуками — сделка [з’д’элка], молотьба [малад’ба]
Правильное написание парных согласных по звонкости/глухости — это орфограмма, которая требует проверочного слова.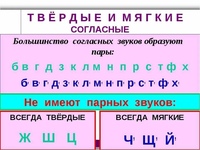
Непарные по звонкости/глухости согласные звуки не оглушаются и не озвончаются, независимо от того, в каком месте слова или перед какими звуками (звонкими или глухими) они находятся.
Например: сор [сор], дом [дом], корка [корка], Димка [димка]
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Мягкие и твёрдые согласные
Алфавит
Гласные звуки и буквы, их обозначающие
Согласные звуки и буквы, их обозначающие
Слог
Ударение
Фонетический разбор
Звуки и буквы
Правило встречается в следующих упражнениях:
1 класс
Страница 48, Канакина, Горецкий, Рабочая тетрадь
Упражнение 210, Климанова, Макеева, Учебник
Страница 55, Климанова, Рабочая тетрадь
Страница 57, Климанова, Рабочая тетрадь
Упражнение 98, Полякова, Учебник
Упражнение 99, Полякова, Учебник
Упражнение 100, Полякова, Учебник
Упражнение 4, Иванов, Евдокимова, Кузнецова, Учебник
Упражнение 5, Иванов, Евдокимова, Кузнецова, Учебник
Упражнение 6, Иванов, Евдокимова, Кузнецова, Учебник
2 класс
Упражнение 20, Канакина, Рабочая тетрадь, часть 2
Упражнение 28, Канакина, Рабочая тетрадь, часть 2
Упражнение 29, Канакина, Рабочая тетрадь, часть 2
Упражнение 172, Климанова, Бабушкина, Учебник, часть 1
Упражнение 189, Климанова, Бабушкина, Учебник, часть 1
Упражнение 24, Полякова, Учебник, часть 2
Упражнение 26, Полякова, Учебник, часть 2
Упражнение 73, Полякова, Учебник, часть 2
Упражнение 120, Полякова, Учебник, часть 2
Упражнение 5, Иванов, Евдокимова, Кузнецова, Петленко, Романова, Учебник, часть 1
3 класс
Упражнение 209, Канакина, Горецкий, Учебник, часть 1
Упражнение 92, Канакина, Рабочая тетрадь, часть 1
Упражнение 42, Климанова, Бабушкина, Учебник, часть 1
Упражнение 46, Климанова, Бабушкина, Учебник, часть 1
Упражнение 187, Полякова, Учебник, часть 1
Упражнение 188, Полякова, Учебник, часть 1
Упражнение 196, Полякова, Учебник, часть 1
Упражнение 202, Полякова, Учебник, часть 1
Упражнение 3, Бунеев, Бунеева, Пронина, Учебник, часть 1
Упражнение 3, Исаева, Бунеев, Рабочая тетрадь
4 класс
Упражнение 8, Бунеев, Бунеева, Пронина, Учебник, часть 1
Упражнение 8, Бунеев, Бунеева, Пронина, Учебник, часть 1
Упражнение 1, Бунеев, Бунеева, Пронина, Учебник, часть 1
Упражнение 433, Ладыженская, Баранов, Тростенцова, Григорян, Кулибаба, Учебник, часть 2
5 класс
Упражнение 30, Разумовская, Львова, Капинос, Учебник
Упражнение 187, Разумовская, Львова, Капинос, Учебник
Упражнение 216, Разумовская, Львова, Капинос, Учебник
Упражнение 34, Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
Упражнение Задачка стр.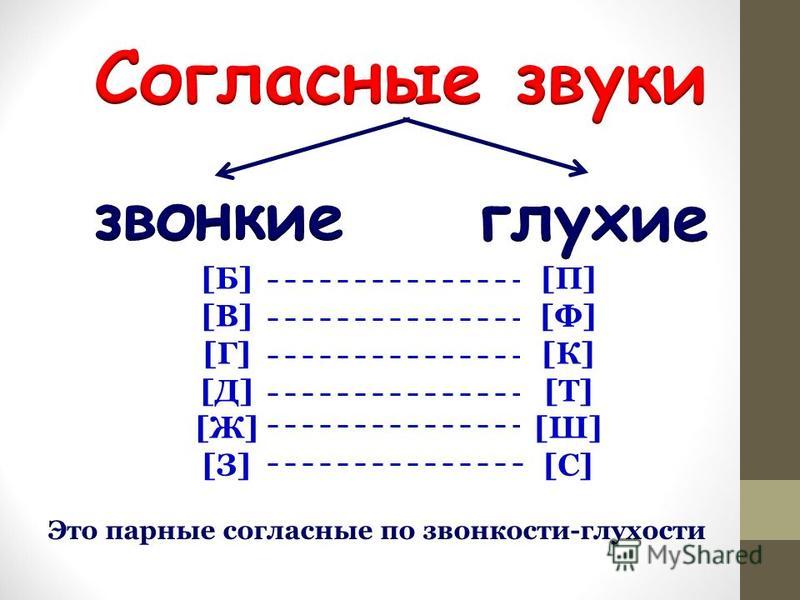 19,
Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
19,
Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
Упражнение 35, Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
Упражнение Задачка стр. 20, Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
Упражнение 36, Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
Упражнение 39, Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
Упражнение Повторение § 10 стр. 38-39, Александрова, Рыбченкова, Глазков, Лисицин, Учебник, часть 1
6 класс
Упражнение 22, Александрова, Рыбченкова, Загоровская, Нарушевич, Учебник, часть 1
7 класс
Упражнение 481, Ладыженская, Баранов, Тростенцова, Григорян, Кулибаба, Александрова, Учебник
Упражнение 36, Разумовская, Львова, Капинос, Учебник
Упражнение 550, Разумовская, Львова, Капинос, Учебник
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
Сонорные звуки в русском языке / Справочник :: Бингоскул
Среди 42-х фонем русского языка 36 – согласные звуки. Это звуки, в образовании которых в большей степени участвуют элементы ротовой полости: язык, губы, зубы, нёбо. В отличие от гласных они состоят из шума. Гласные – только из голоса, так как в их образовании участвуют легкие и голосовые связки. Но не все согласные в одинаковой степени состоят из шума. Среди них есть такие, в которых присутствует значительная часть голоса. Они называются звонкими согласными.
Классификация согласных звуков
По уровню шума:
| По уровню шума | |
| Сонорные | — преобладает голос, уровень шума незначительный — [л], [м], [н], [р], [й]; |
| Шумные | — значительный уровень шума. Шумные делятся на:
|
| По твердости | |
| Твердые | [л], [д], [с], [ж], [ц], [ш] и др. |
| Мягкие | [л,], [д,], [с,], [ш,], [ч,], [й] и др. |
Среди звонких согласных насчитывается 9 звуков, в которых голоса больше, чем шума. Это сонорные звуки.
Определение
Сонорные звуки – это звонкие согласные звуки, в которых голос доминирует над шумом.
Слово «сонорный» происходит от латинского – «sonorous», что в переводе на русский значит – «звонкий». Группа сонорных включает в свой состав восемь парных по мягкости – твердости и один мягкий непарный: [л] – [л’], [м] – [м’], [н] – [н’], [р] – [р’], [й].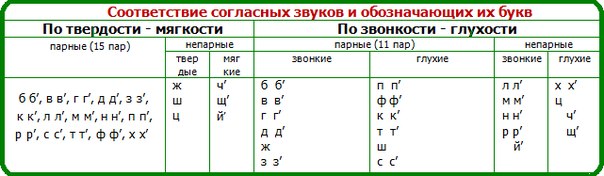
Сонорные звуки, как правило, образуются при участии легких, голосовых связок, губ, языка, нёба. Зубы в их образовании не участвуют. По месту и способу образования они бывают: губно-губные – [м], [м’]; язычно-губные – [н], [н’]; язычно-небные – [л], [л’], [р], [р’], [й’]. По силе звука все они являются звонкими.
Непарные звонкие сонорные звуки
Как было отмечено выше, все сонорные относятся к звонким согласным звукам. В отличие от большинства звонких согласных, сонорные звуки не имеют пар по глухости. Если другие согласные, как например, [д], [д‘], [б], [б‘], [з], [з‘] и другие имеют парные глухие [т], [т‘], [п], [п‘], [с], [с‘], то сонорные звуки [л], [л’], [м], [м’], [н], [н’], [р], [р’], [й’] такой пары среди глухих согласных не имеют. Все сонорные звуки по этому признаку – непарные. Они ни в какой позиции не оглушаются: ни в конце слова, ни перед глухими согласными. Всегда произносятся звонко – с голосовой силой, а обычные парные согласные в конце слова и перед глухим согласными произносятся глухо.
Это легко проверить в сравнении:
«дом»: до[м] – «мороз»: моро[с]; «день»: де[н’] – «медь»: ме[т’]; «поломка»: поло[м]ка – лодка: ло[т]ка; «долька»: до[л’]ка – «редька»: ре[т’]ка.
- Согласные Р, Л, М, Н, Й называются — сонорными.
- Все только звонкие, непарные согласные помогает запомнить фраза:
ЛИМОН — РАЙ!
Если в данном предложении вычеркнуть все гласные, то останутся только звонкие, непарные согласные звуки.
| Твердые сонорные звуки | Сонорные звуки, за исключением звука [й’], имеют пару по твердости: [л] – [л’], [м] – [м’], [н] – [н’], [р] – [р’]. В определенных позициях могут произноситься и мягко, и твердо: «лось»: [л]ось – «соль»: со[л‘]; «моль»: [м]оль – «мель»: [м’]ель; «дно»: д[н]о – «день»: де[н‘], «рысь»: [р]ысь – «дверь»: две[р‘]. Звук [й’] ни при каких условиях твердо не произносится, не имеет пары по твердости: «яйцо» – [й’ай’цо]. |
| Звонкие сонорные согласные звуки | Все сонорные только звонкие звуки, глухих звуков среди них не имеется!!! |
| Глухие сонорные звуки | Среди сонорных глухих звуков нет!!! |
| Шипящие сонорные звуки | Шипящих сонорных звуков не бывает!!! |
Таблица сонорных звуков
Что значит «сонорный» в фонетическом разборе?
Сонорные звуки в фонетическом разборе представляет собой согласные непарные по звонкости – глухости. Парными они бывают по твердости – мягкости. Звук [й’] не имеет пары по мягкости – твердости, звонкости – глухости, звуки он только звонкий и только мягкий. В зависимости от позиции, занимаемой в слове, сонорные – [л] – [л’], [м] – [м’], [н] – [н’], [р] – [р’] – при звуко-буквенном разборе имеют следующую характеристику: «согласный, сонорный.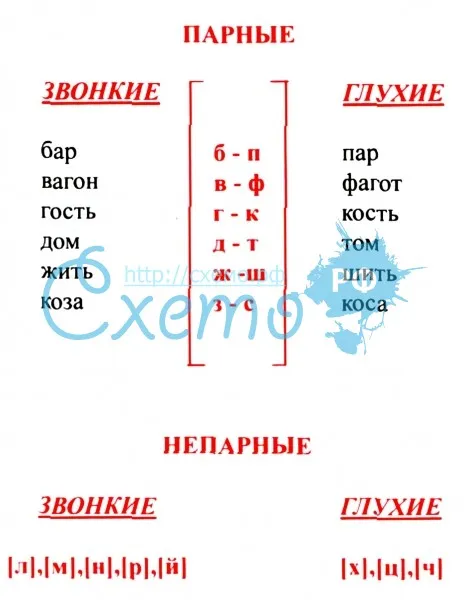 , звонкий непарный, мягкий парный». Характеристика звука [й‘] несколько отличается, так как этот звук не имеет пары по твердости. Его характеристика неизменна – «согласный, сонорный, звонкий непарный, мягкий непарный». Иногда к словам «звонкий» и «мягкий» добавляют – «только» или «всегда».
, звонкий непарный, мягкий парный». Характеристика звука [й‘] несколько отличается, так как этот звук не имеет пары по твердости. Его характеристика неизменна – «согласный, сонорный, звонкий непарный, мягкий непарный». Иногда к словам «звонкий» и «мягкий» добавляют – «только» или «всегда».
Смотри также:
Фонетический разбор | Русский язык
1. Фонетический разбор слова осуществляется по следующей схеме:
2. Затранскрибировать слово, поставив ударение.
3. На транскрипции дефисами (или вертикальными линиями) обозначить слогораздел.
4. Определить количество слогов, указать ударный.
5. Показать, какому звуку соответствует каждая буква. Определить количество букв и звуков.
6. В столбик выписать буквы слова, рядом — звуки, указать их соответствие.
7. Указать количество букв и звуков.
Охарактеризовать звуки по следующим параметрам:
· гласный: ударный / безударный;
· согласный: глухой / звонкий с указанием парности, твёрдый / мягкий с указанием парности.
Образец фонетического разбора:
его [й’и-вo] 2 слога, второй ударный
[й’] согласный, звонкий непарный, мягкий непарный
е — [и] гласный, безударный
г — [в] согласный, звонкий парный, твёрдый парный
о — [́о] гласный, ударный
3 б., 4 зв.
В фонетическом разборе показывают соответствие букв и звуков, соединяя буквы с обозначаемыми ими звуками (за исключением обозначения твёрдости / мягкости согласного последующей гласной буквой). Поэтому необходимо обратить внимание на буквы, обозначающие два звука, и на звуки, обозначаемые двумя буквами. Особое внимание надо уделить мягкому знаку, который в одних случаях обозначает мягкость предшествующего парного согласного (и в этом случае он, как и предшествующая ему согласная буква, соединяется с согласным звуком), а в других случаях не несёт фонетической нагрузки, выполняя грамматическую функцию (в этом случае рядом с ним в транскрипционных скобках ставится прочерк), например:
к — [к]
н — [н]
о — [о]
о — [о]
н — [н’]
ч — [ч’]
ь
ь — [ — ]
Обратите внимание на то, что у согласных звуков парность указывается отдельно по признаку глухости / звонкости и по признаку твёрдости / мягкости, поскольку в русском языке представлены не только абсолютно непарные согласные ([й’], [ц], [ч’], [щ’]), но и согласные, непарные только по одному из этих признаков, например: [л] — звонкий непарный, твёрдый парный, [ж] — звонкий парный, твёрдый непарный.
Фонетический разбор слова. Начальная школа.
Что надо знать для фонетического разбора слов в начальной школе.
Фонетика – раздел науки о языке, в котором изучаются звуки речи.
Буквы – это графические знаки, с помощью которых звуки речи обозначаются при письме.
Звуки мы произносим и слышим, буквы – видим и пишем. Читая слова, мы видим буквы, а произносим звуки.
Звуки бывают гласные и согласные.
Гласные звуки.
При произнесении гласных выдыхаемый воздух свободно выходит изо рта и не встречает преград. Гласные звуки можно петь. Они состоят только из голоса, который образуется при дрожании голосовых связок.
В русском языке 10 гласных букв: А-Я,О-Ё, У-Ю, Ы-И, Э-Е,
но 6 гласных звуков: [А], [О], [У], [Ы], [ Э], [И].
- А, О, У, Ы, Э – это буквы, которые дают предыдущему согласному команду: «Читайся твёрдо!», но звуки [ч’], [щ’] – всегда мягкие:
сон [сон], дым [дым], чаща [ч’ащ’а], часы [ч’асы].
- Я, Ё, Ю, И, Е – это буквы, которые дают предыдущему согласному команду: «Читайся мягко!» (обозначают мягкость предыдущего согласного), но звуки [ж], [ш], [ц] остаются всегда твердыми:
мята [м’ата], тёрка [т’орка], мюсли [м’усл‘и], мел [м’эл], лес [л’эс], жир [жыр], ширь [шыр’], цифра [цыфра].
- Буквы Я, Ё, Ю, Е – йотированные. Они могут давать один или два звука, в зависимости от положения в слове.
- Я, Ё, Ю, Е стоят после согласных, то обозначают мягкость предыдущего согласного (кроме всегда твердых [ж], [ш], [ц]) и дают один гласный звук : я – [а], ё – [о], ю – [у], е – [э] :
Мяч[м‘ач], тёрн [т‘орн], тюль [т‘ул’], пена [п‘эна].
- Я, Ё, Ю, Е дают два звука: согласный [й’] и соответствующий гласный, если они стоят
- в начале слова: яма [й’aма ], ёлка [й’олка], юла [й’у ла ], ель [й’э л’];
- после гласных: маяк [май’ак], поёт [пай’от], поют [пай’ут], поел [пай’эл];
- после разделительных Ъ и Ь знаков: деревья [д’ир’эв’й’а ], объём [абй’ом], вьюга [вй’уга], съезд [сй’эст].
- Я, Ё, Ю, Е стоят после согласных, то обозначают мягкость предыдущего согласного (кроме всегда твердых [ж], [ш], [ц]) и дают один гласный звук : я – [а], ё – [о], ю – [у], е – [э] :
- В транскрипции буквы Я, Ё, Ю, Е не используются. Звуков [е], [ё], [ю], [я] не существует.
- Буква И после Ь обозначает два звука: чьи [ч’й’и], лисьи [лис’й’и]
- [й’] – согласный, всегда звонкий, всегда мягкий звук .

В состав слога обязательно входит гласный звук: “Сколько в слове гласных, столько и слогов. Это знает каждый из учеников!”
Для малышей! Чтобы определить количество слогов в слове, надо приложить раскрытую ладошку под подбородок и четко произнести слово. На гласных подбородок ударит по ладошке. Посчитайте количество таких ударов и узнаете количество слогов.
Согласные звуки.
При произнесении согласных выдыхаемый воздух встречает преграды (губы, зубы и язык) в ротовой полости. Всего 36 согласных звуков.
Согласные звуки бывают твердые и мягкие, звонкие и глухие.
- Звонкие
- образуются при помощи голоса (вибрируют голосовые связки) и шума.
- Л, М, Н, Р, Й – самые звонкие согласные (больше голоса и совсем мало шума в звуке), всегда звонкие.
- Б, В, Г, Д, Ж, З – звонкие [б], [в], [г], [д], [ж], [з], [б’], [в’], [г’], [д’], [з’], имеют парные звуки по звонкости/глухости.

- Фраза для запоминания содержит все звонкие согласные: Мы же не забывали друга.
- Глухие
- произносятся без голоса (без колебания голосовых связок) и состоят только из шума:
- П, Ф, К, Т, Ш, С – глухие [п], [ф], [к], [т], [ш], [с], [п’], [ф’], [к’], [т’], [с’] имеют парные звонкие;
- X, Ц, Ч, Щ – [х], [х’], [ц], [ч’], [щ’] – всегда глухие, не имеют парных по звонкости/глухости .
- Фразы для запоминания, которые содержат все глухие согласные:
- «Степка, хочешь щец?» – «Фи!»
- Фока, хочешь поесть щец?
Для того чтобы определить, звонкий или глухой согласный, ребёнок закрывает уши ладошками и произносит этот звук. Если ребёнок при произнесении слышит голос, то это звонкий согласный.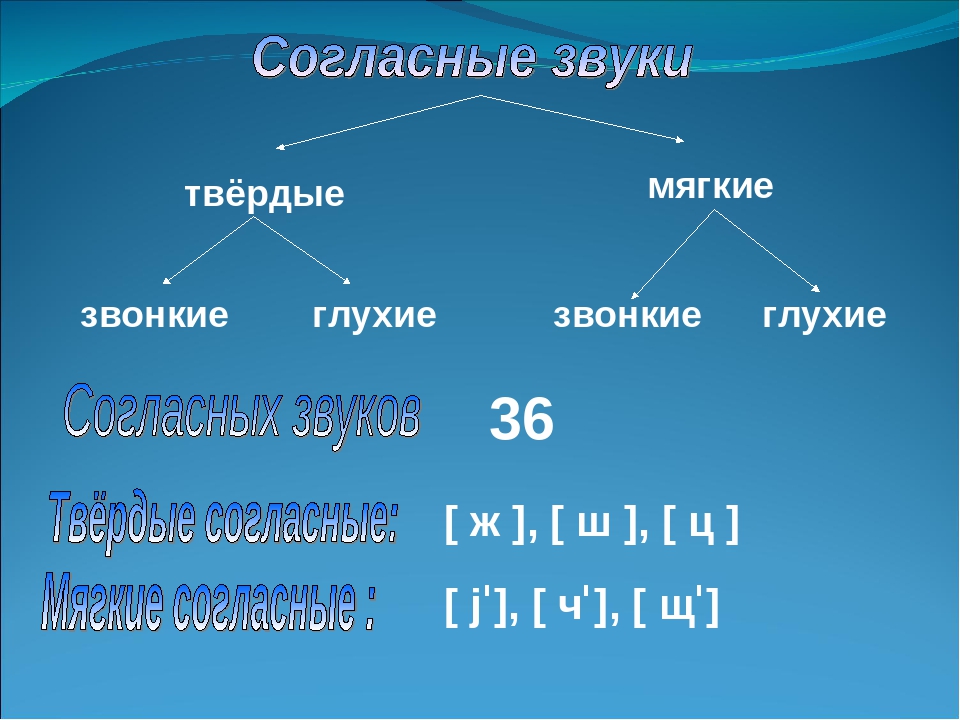 Если слышит не голос, а шум, то этот согласный глухой.
Если слышит не голос, а шум, то этот согласный глухой.
- Твердые: [б], [в], [г], [д], [ж], [з], [к], [л], [м], [н], [п], [р], [с], [т], [ф], [х], [ц], [ш].
- Мягкие: [б’], [в’], [г’], [д’], [з’], [й’], [к’], [л’], [м’], [н’], [п’], [р’], [с’], [т’], [ф’], [х’], [ч’], [щ’]. При фонетическом разборе мягкие звуки обозначаются знаком [‘].
Твердые и мягкие согласные при произношении различаются положением языка. Важно различать для правильного произношения и написания слов: мол [мол] – моль [мол’], угол [угол] – уголь [угол’], нос [нос] – нёс [н’ос].
- Л, М, Н, Р, Й – всегда звонкие.
- Б-П, В-Ф, Г-К, Д-Т, Ж-Ш, З-С – парные согласные по звонкости-глухости.
- X, Ц, Ч, Щ – всегда глухие согласные.
- Ч, Щ, Й – всегда мягкие согласные.
- Ж, Ш, Ц – всегда твердые согласные.

- Ж, Ш,Ч, Щ – шипящие.
ФОНЕТИЧЕСКИЙ (ЗВУКО-БУКВЕННЫЙ) АНАЛИЗ СЛОВА
- Запишите слово.
- Поставьте ударение.
- Разделите слово на слоги. Сосчитайте и запишите их количество.
- Выпишите все буквы этого слова в столбик одну под другой. Сосчитайте и запишите их количество.
- Напишите справа от каждой буквы, в квадратных скобках, звук, который эта буква обозначает.
- Опишите звуки:
- Гласный, ударный или безударный.
- Согласный, глухой или звонкий, парный или непарный; твёрдый или мягкий, парный или непарный.
- Сосчитайте и запишите количество звуков.
- Иногда требуется объяснить особенности правописания (орфографические правила).
Примеры
| ко|леч|ко – 3 слога, 7 б., 7 зв. | ||
|---|---|---|
| К | [к] | согл., глух., тв. |
| О | [а] | глас, безудар. |
| Л | [л’] | согл., звон., мягк. |
| Е | [э] | глас, удар. |
| Ч | [ч’] | согл., глух., мягк. |
| К | [к] | согл., глух., тв. |
| О | [а] | глас, безудар. |
| Ель – 1 слог, 3 б. 3 зв. | ||
| Е | [й’] | согл., звон., мягк. |
| [э] | глас, удар. | |
| Л | [л’] | согл., звон., мягк. |
| Ь | [-] | не обозначает звука, обозначает мягкость предыдущего согласного звука Л |
Обратите внимание !
Для гласных.
- Буквы Я, Ё, Ю, Е – йотированные.
- Если эти буквы стоят после согласных, то они дают один звук:
- Я – [а], Ё – [о], Ю – [у], Е – [э]: Лён – [л’ о н] – 3 буквы, 3 звука.
- Если эти буквы стоят в начале слова, после гласных и разделительных Ъ и Ь знаков, то они дают 2 звука:
- Я – [й’а], Ё – [й’о], Ю – [й’у], Е – [й’э]: Ёлка – [й’ о л к а] – 4 буквы, 5 звуков.
 Поёт [пай’о т ] – 4 буквы, 5 звуков.
Поёт [пай’о т ] – 4 буквы, 5 звуков.
- Я – [й’а], Ё – [й’о], Ю – [й’у], Е – [й’э]: Ёлка – [й’ о л к а] – 4 буквы, 5 звуков.
- Если эти буквы стоят после согласных, то они дают один звук:
- Буква И
- после Ь обозначает два звука: чьи [ч’й’и], лисьи [лис’й’и];
- после согласных Ж, Ш, Ц даёт звук [ы]:
- зажим [зажым], шины [ш ы н ы], цирк [цырк] ;
- гласная О под ударением даёт звук [о], а без ударения [а]:
- кОтик – [ кОт ‘ и к], скворцы – [с к в а р ц ы];
- гласная Е под ударением даёт звук [э], а без ударения [и]:
- лес [л’эс], лесА [л’исА] (см. лисА [л’исА]), весна [в’исна];
- в некоторых иноязычных словах перед гласной Е согласный произносится твёрдо:
- кафе [кафэ], купе [купэ], свитер [свитэр], отель [атэл’];
- гласная Я под ударением даёт звук [а], а без ударения [э], [и]:
- мяч – [м’ач’], рябина – [р’эб’ина], пятно – [п’итно].

- мяч – [м’ач’], рябина – [р’эб’ина], пятно – [п’итно].
- Буквы Я, Ё, Ю, Е – йотированные.
Для согласных.
- парные по глухости/звонкости согласные в конце слова, перед глухой согласной произносятся глухо (оглушаются):
- гриб – [гр’ и п], лавка – [л а ф к а];
- Й, Ч, Щ – [й’], [ч’], [щ’] – всегда мягкие;
- Ж, Ш, Ц – [ж], [ш], [ц] – всегда твердые;
- Если в слове рядом стоят несколько согласных, то в некоторых словах звуки [в], [д], [л], [т] не произносятся (непроизносимые согласные), но буквы в,д, л, т пишутся:
- чувство [ч’Уства], солнце [сОнцэ], сердце [с’Эрцэ], радостный [рАдасный’].
- сочетание СТН произносится как [сн], ЗДН – [зн]:
- звёздный – [з в’ о з н ы й’], лестница – [л’ эс ‘н’и ц а].

- звёздный – [з в’ о з н ы й’], лестница – [л’ эс ‘н’и ц а].
- иногда на месте буквы Г перед глухой согласной произносятся звуки [к], [х]:
- когти – [к о к т’ и], мягкий – [м’ ах ‘ к ‘ и й’];
- иногда буква С в начале слова перед звонкой согласной озвончается:
- сделал – [з’ д’ э л а л].
- между корнем и суффиксом перед мягкими согласными согласные могут звучать мягко :
- зонтик – [з о н’ т ‘и к];
- иногда буква Н обозначает мягкий согласный звук перед согласными Ч, Щ:
- стаканчик – [с т а к а н’ ч’ и к], сменщик – [см’э н’ щ’ и к];
- Удвоенные согласные располагаются
- после ударного гласного, то дают длинный звук : грУппа [ груп:а], вАнна [ ван:а];
- перед ударным гласным, то образуется обычный согласный звук: миллиОн [м’ил‘иОн], аккОрд [акОрт], аллЕя [ал‘Эй’а] ;
- сочетания ТСЯ, ТЬСЯ (у глаголов) произносятся как длинный [ц]:
- бриться – [бр’ иц:а];
- иногда сочетание ЧН, ЧТ произносится как [ш]:
- конечно – [ кан ‘ эшна ], скучно – [ скушна ], что – [ш т о], чтобы – [штобы];
- буква Щ и сочетания букв СЧ, ЗЧ, ЖЧ обозначают звук [щ’]:
- щавель [щ ‘ав ‘ эл ‘ ], счастливый [ щ ‘асливый ‘ ], извозчик [извощ ‘ик], перебежчик [п ‘ир ‘иб’Эщ ‘ик];
- в окончаниях имён прилагательных ОГО, ЕГО согласный Г произносится как [в]:
- белого – [б’ Э л а в а].

- белого – [б’ Э л а в а].
- парные по глухости/звонкости согласные в конце слова, перед глухой согласной произносятся глухо (оглушаются):
1-выборочный, 2-выборочный и парный t-тесты
В статистике t-тесты представляют собой тип проверки гипотезы, который позволяет сравнивать средние значения. Они называются t-тестами, потому что каждый t-тест сводит ваши выборочные данные к одному числу — t-значению. Если вы понимаете, как t-тесты вычисляют t-значения, вы хорошо на пути к пониманию того, как эти тесты работают.
В этой серии публикаций я сосредотачиваюсь на концепциях, а не на уравнениях, чтобы показать, как работают t-тесты. Однако этот пост включает два простых уравнения, над которыми я буду работать, используя аналогию отношения сигнал / шум.
Minitab Statistical Software предлагает t-критерий для 1 выборки, парный t-критерий и t-критерий для 2 выборок. Давайте посмотрим, как каждый из этих t-тестов сокращает ваши выборочные данные до t-значения.
Как t-тесты с одной выборкой вычисляют t-значения
Понимание этого процесса имеет решающее значение для понимания того, как работают t-тесты.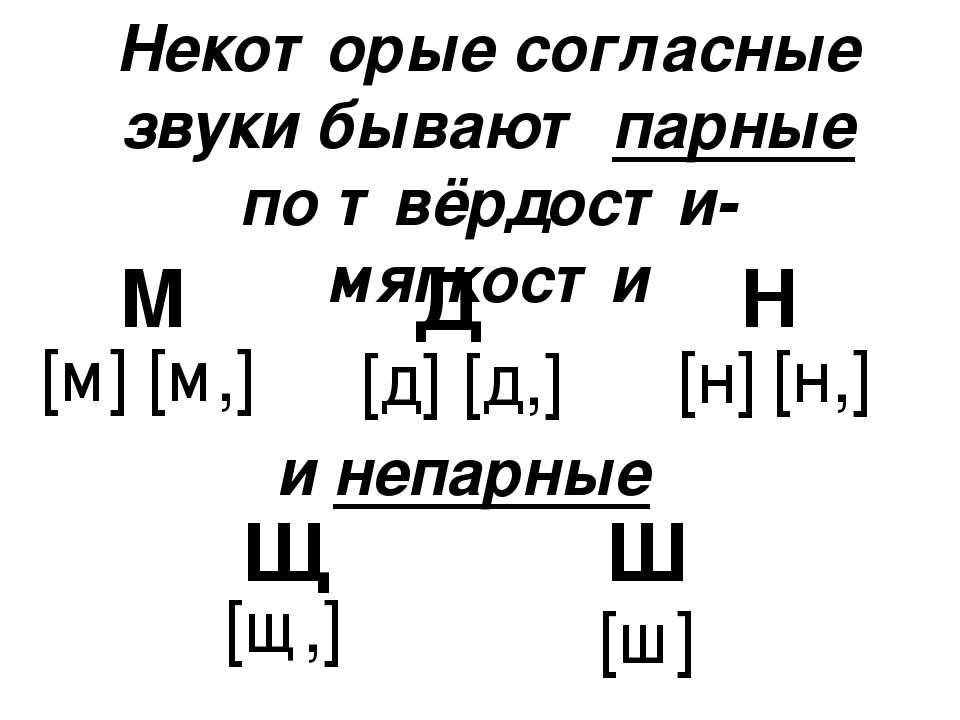 Сначала я покажу вам формулу, а затем объясню, как она работает.
Сначала я покажу вам формулу, а затем объясню, как она работает.
Обратите внимание, что формула является соотношением. Общая аналогия заключается в том, что значение t — это отношение сигнал / шум.
Сигнал (он же размер эффекта)В числителе стоит сигнал. Вы просто берете среднее значение выборки и вычитаете значение нулевой гипотезы. Если среднее значение вашей выборки равно 10, а нулевая гипотеза равна 6, разница или сигнал составляет 4.
Если нет разницы между выборочным средним и нулевым значением, сигнал в числителе, а также значение всего отношения равны нулю. Например, если среднее значение вашей выборки равно 6, а нулевое значение — 6, разница равна нулю.
По мере того, как разница между средним значением выборки и средним значением нулевой гипотезы увеличивается в положительном или отрицательном направлении, сила сигнала увеличивается.
Сильный шум может заглушить сигнал. Шум
Знаменатель — это шум. Уравнение в знаменателе — это мера изменчивости, известная как стандартная ошибка среднего. Эта статистика показывает, насколько точно ваша выборка оценивает среднее значение генеральной совокупности.Большее число указывает на то, что ваша выборочная оценка менее точна, поскольку в ней больше случайных ошибок.
Уравнение в знаменателе — это мера изменчивости, известная как стандартная ошибка среднего. Эта статистика показывает, насколько точно ваша выборка оценивает среднее значение генеральной совокупности.Большее число указывает на то, что ваша выборочная оценка менее точна, поскольку в ней больше случайных ошибок.
Эта случайная ошибка и есть «шум». Когда шума больше, вы ожидаете увидеть большие различия между выборочным средним и значением нулевой гипотезы , даже если нулевая гипотеза верна. Мы включаем коэффициент шума в знаменатель, потому что мы должны определить, достаточно ли велик сигнал, чтобы выделяться из него.
Отношение сигнал / шум Значения как сигнала, так и шума выражаются в единицах ваших данных.Если ваш сигнал равен 6, а шум равен 2, ваше t-значение равно 3. Это t-значение указывает, что разница в 3 раза превышает размер стандартной ошибки. Однако, если есть разница такого же размера, но ваши данные более изменчивы (6), ваше t-значение будет только 1. Сигнал находится в том же масштабе, что и шум.
Сигнал находится в том же масштабе, что и шум.
Таким образом, t-значения позволяют вам увидеть, насколько ваш сигнал отличается от шума. Относительно большие сигналы и низкий уровень шума дают большие t-значения. Если сигнал не выделяется из шума, вполне вероятно, что наблюдаемое различие между оценкой выборки и значением нулевой гипотезы вызвано случайной ошибкой в выборке, а не истинной разницей на уровне совокупности.
Парный t-тест — это всего лишь t-тест для 1 выборки
Многие люди не понимают, когда использовать парный t-критерий и как он работает. Открою вам маленький секрет. Парный t-критерий и t-критерий для 1 выборки фактически являются одним и тем же замаскированным тестом! Как мы видели выше, t-критерий для 1 выборки сравнивает среднее значение одной выборки со значением нулевой гипотезы. Парный t-критерий просто вычисляет разницу между парными наблюдениями (например, до и после), а затем выполняет 1-выборочный t-критерий для различий.
Вы можете проверить это с помощью этого набора данных, чтобы увидеть, насколько все результаты идентичны, включая среднюю разницу, t-значение, p-значение и доверительный интервал разницы.
Понимание того, что парный t-тест просто выполняет t-тест с одной выборкой для парных различий, действительно может помочь вам понять, как работает парный t-тест и когда его использовать. Вам просто нужно выяснить, имеет ли смысл вычислять разницу между каждой парой наблюдений.
Например, предположим, что «до» и «после» представляют собой результаты теста, и между ними было вмешательство. Если оценки «до» и «после» в каждой строке примера рабочего листа представляют один и тот же предмет, имеет смысл рассчитать разницу между оценками таким образом — подходит парный t-критерий. Однако, если баллы в каждой строке выставлены по разным предметам, нет смысла вычислять разницу. В этом случае вам нужно будет использовать другой тест, например, двухвыборочный t-критерий, о котором я расскажу ниже.
Использование парного t-критерия просто избавляет вас от необходимости вычислять различия перед выполнением t-критерия. Вам просто нужно убедиться, что парные различия имеют смысл!
Когда уместно использовать парный t-критерий, он может быть более мощным, чем t-критерий с двумя выборками. Для получения дополнительной информации перейдите в Обзор для парных t.
Для получения дополнительной информации перейдите в Обзор для парных t.
Как двухвыборочные T-тесты вычисляют T-значения
Двухвыборочный t-критерий берет данные вашей выборки из двух групп и сводит их к t-значению.Этот процесс очень похож на t-тест для 1 выборки, и вы все равно можете использовать аналогию отношения сигнал / шум. В отличие от парного t-критерия, t-критерий для двух выборок требует независимых групп для каждой выборки.
Формула ниже, а затем некоторое обсуждение.
Для t-критерия с двумя выборками числитель снова является сигналом, который представляет собой разницу между средними значениями двух выборок. Например, если среднее значение группы 1 равно 10, а среднее значение группы 2 равно 4, разница составляет 6.
Нулевая гипотеза по умолчанию для двухвыборочного t-критерия состоит в том, что две группы равны. Вы можете видеть в уравнении, что, когда две группы равны, разница (и все соотношение) также равно нулю. По мере того, как разница между двумя группами увеличивается в положительном или отрицательном направлении, сигнал становится сильнее.
В t-тесте с двумя выборками знаменателем по-прежнему является шум, но Minitab может использовать два разных значения. Вы можете предположить, что изменчивость в обеих группах равна или не равна, и Minitab использует соответствующую оценку изменчивости.В любом случае принцип остается тем же: вы сравниваете свой сигнал с шумом, чтобы увидеть, насколько сигнал выделяется.
Как и в случае с t-критерием для 1 выборки, для любой заданной разницы в числителе, когда вы увеличиваете значение шума в знаменателе, t-значение становится меньше. Чтобы определить, что группы разные, вам нужно большое значение t.
Что означают t-значения?
Каждый тип t-теста использует процедуру для сведения всех ваших выборочных данных к одному значению, t-значению.В ходе расчетов среднее (-ые) ваше выборочное среднее (-я) сравнивается с нулевой гипотезой и учитывается как размер выборки, так и изменчивость данных. Значение t, равное 0, указывает, что результаты выборки точно соответствуют нулевой гипотезе. В статистике мы называем разницу между оценкой выборки и нулевой гипотезой величиной эффекта. По мере увеличения этой разницы абсолютное значение t-значения увеличивается.
В статистике мы называем разницу между оценкой выборки и нулевой гипотезой величиной эффекта. По мере увеличения этой разницы абсолютное значение t-значения увеличивается.
Это все хорошо, но что на самом деле означает значение t, скажем, 2? Из приведенного выше обсуждения мы знаем, что значение t, равное 2, указывает на то, что наблюдаемая разница в два раза превышает размер изменчивости ваших данных.Однако мы используем t-тесты для оценки гипотез, а не просто для определения отношения сигнал / шум. Мы хотим определить, является ли величина эффекта статистически значимой.
Чтобы увидеть, как мы переходим от t-значений к оценке гипотез и определению статистической значимости, прочитайте другой пост в этой серии, «Понимание t-тестов: t-значения и t-распределения».
Парный и непарный T-тест: различия, предположения и гипотезы
Двухвыборочный t-тест — это статистические тесты, используемые для сравнения средних значений двух популяций.Их результаты, также известные как t-критерии Стьюдента, используются, чтобы определить, существует ли значительная разница между средним значением двух выборок, которая, скорее всего, не связана с ошибкой выборки или случайной случайностью.
t-критерии Стьюдента делятся на две категории: парные t-критерии и непарные t-критерии. Эти статистические тесты обычно используются в исследованиях в области биологии, бизнеса и психологии.
В этой статье объясняется, когда уместно использовать парный t-критерий по сравнению с непарным t-критерием, а также гипотезы и предположения каждого из них.
Что такое парный t-критерий?
Парный t-критерий (также известный как зависимый или коррелированный t-критерий) — это статистический тест, который сравнивает средние / средние значения и стандартные отклонения двух связанных групп, чтобы определить, есть ли значительная разница между двумя группами.
● Значительная разница возникает, когда различия между группами маловероятны из-за ошибки выборки или случайности.
● Группы могут быть связаны между собой, являясь одной и той же группой людей, одним и тем же элементом или находясь в одинаковых условиях.
Парные t-тесты считаются более эффективными, чем непарные t-тесты, потому что использование одних и тех же участников или элементов устраняет различия между выборками, которые могут быть вызваны чем-либо, кроме того, что тестируется.
Каковы гипотезы парного t-критерия?
В парном t-тесте возможны две гипотезы.
● Нулевая гипотеза (H0) утверждает, что нет существенной разницы между средними значениями двух групп.
● Альтернативная гипотеза (h2) утверждает, что существует значительная разница между двумя средними значениями генеральной совокупности, и что эта разница вряд ли будет вызвана ошибкой выборки или случайностью.
Каковы предположения парного t-критерия?
● Зависимая переменная с нормальным распределением
● Наблюдения выбираются независимо
● Зависимая переменная измеряется на инкрементальном уровне, например, с отношениями или интервалами.
● Независимые переменные должны состоять из двух связанных групп или согласованных пар.
Когда использовать парный t-тест?
Парные t-критерии используются, когда один и тот же элемент или группа проверяется дважды, что известно как t-критерий повторных измерений. Некоторые примеры случаев, для которых подходит парный t-тест, включают:
Некоторые примеры случаев, для которых подходит парный t-тест, включают:
● Эффект до и после фармацевтического лечения на одну и ту же группу людей.
● Температура тела с использованием двух разных термометров для одной и той же группы участников.
● Стандартизированные результаты тестирования группы студентов до и после курса подготовки к обучению.
Что такое непарный t-критерий?
Непарный t-критерий (также известный как независимый t-критерий) — это статистическая процедура, которая сравнивает средние / средние значения двух независимых или несвязанных групп, чтобы определить, есть ли между ними значительная разница.
Каковы гипотезы непарного t-критерия?
Гипотезы для непарного t-критерия такие же, как и для парного t-критерия. Это две гипотезы:
● Нулевая гипотеза (H0) утверждает, что нет существенной разницы между средними значениями двух групп.
● Альтернативная гипотеза (h2) утверждает, что существует значительная разница между двумя средними значениями генеральной совокупности, и что эта разница вряд ли будет вызвана ошибкой выборки или случайностью.
Каковы предположения непарного t-критерия?
● Зависимая переменная с нормальным распределением
● Наблюдения выбираются независимо
● Зависимая переменная измеряется на инкрементальном уровне, например, с отношениями или интервалами.
● Дисперсия данных между группами одинакова, что означает, что они имеют одинаковое стандартное отклонение
● Независимые переменные должны состоять из двух независимых групп.
Когда использовать непарный t-критерий?
Непарный t-критерий используется для сравнения среднего значения между двумя независимыми группами. Вы используете непарный t-тест, когда сравниваете две отдельные группы с равной дисперсией.
Примеры подходящих случаев, в которых следует использовать непарный t-критерий:
● Исследование, такое как фармацевтическое исследование или другой план лечения, где ½ субъектов распределяются в группу лечения, а ½ субъектов распределяются случайным образом. в контрольную группу.
● Исследование, в ходе которого есть две независимые группы, такие как женщины и мужчины, которые проверяют, значительно ли различается средняя плотность костной ткани между двумя группами.
● Сравнение среднего расстояния до работы, пройденного жителями Нью-Йорка и Сан-Франциско, с использованием 1000 случайно выбранных участников из каждого города.
В случае неравных отклонений следует использовать критерий Велча.
Парный и непарный t-тест
Ключевые различия между парным и непарным t-тестом приведены ниже.
- Парный t-критерий предназначен для сравнения средних значений одной и той же группы или элемента в двух разных сценариях. Непарный t-критерий сравнивает средние значения двух независимых или несвязанных групп.
- В непарном t-тесте предполагается, что дисперсия между группами одинакова. В парном t-тесте дисперсия не считается равной.
Таблица парного и непарного t-теста
Парный и непарный t-тест — перекрестная проверка
Теперь я намного лучше понимаю, что меня беспокоило по поводу парных и непарных t-тестов и связанных p-значений.Это было интересное путешествие, и на этом пути было много сюрпризов. Один сюрприз стал результатом расследования вклада Майкла. Это безупречный практический совет. Более того, он говорит то, во что, по моему мнению, верят практически все статистики, и у него есть несколько голосов в поддержку этого. Однако как часть теории это не совсем правильно. Я обнаружил это, разработав формулы для p-значений, а затем тщательно подумав, как использовать эти формулы, чтобы привести к контрпримерам.9; numSamples <- 3; pv <- function (vLength, meanDiff) { X <- rnorm (vLength) Y <- X - meanDiff + rnorm (vLength, sd = 0,0001) Парный <- t.test (X, Y, var.equal = T, paired = T) NotPaired <- t.test (X, Y, var.equal = T, paired = F) c (Парное значение $ p., NotPaired $ p.value, cov (X, Y)) } ans <- реплицировать (numSamples, pv (vLength, meanDiff))
Обратите внимание на следующие особенности: X и Y — два кортежа из 10, разница между которыми огромна и почти постоянна. Для многих значащих цифр соотношение равно 1.В 40 раз меньше, чем p-значение для парного теста. Таким образом, это противоречит рассказу Майкла, при условии, что его отчет читать буквально в математическом стиле. Здесь заканчивается часть моего ответа, связанная с ответом Майкла.
Вот мысли, подсказанные ответом Питера. Во время обсуждения моего первоначального вопроса я предположил в комментарии, что два конкретных распределения p-значений, которые звучат по-разному, на самом деле одинаковы. Теперь я могу это доказать. Более важно то, что доказательство раскрывает фундаментальную природу p-значения, настолько фундаментальную, что ни один текст (который я встречал) не удосужился объяснить.Может быть, все профессиональные статистики знают секрет, но мне определение p-значения всегда казалось странным и искусственным. Прежде чем раскрыть секрет статистики, уточню вопрос.
Пусть $ n> 1 $ и случайно и независимо выберут два случайных $ n $ -набора из некоторого нормального распределения. Есть два способа получить p-значение из этого выбора. Один из них — использовать непарный t-критерий, а другой — использовать парный t-критерий. Моя гипотеза заключалась в том, что распределение p-значений, которое мы получаем, одинаково в двух случаях.Когда я впервые начал думать об этом, я решил, что эта гипотеза была безрассудной и ложной: непарный тест связан с t-статистикой по $ 2 (n-1) $ степеням свободы, а парный тест — с t -статистический по $ n-1 $ степеням свободы. Эти два распределения различны, так как же, черт возьми, связанные распределения p-значений могут быть одинаковыми? Только после долгих размышлений я понял, что это очевидное отклонение моей гипотезы было слишком поверхностным.
Ответ исходит из следующих соображений.\ infty f (s) \, ds $$ и это объясняется во многих текстах. Что в текстах не указано в контексте p-значений, так это то, что это , ровно формула, которая дает p-значение из t-статистики, когда $ f $ — это pdf для t-распределения. (Я стараюсь, чтобы обсуждение было как можно более простым, потому что оно действительно простое. Более полное обсуждение будет относиться к односторонним и двусторонним t-критериям немного по-разному, могут возникнуть множители 2, и t-статистика может лежать в $ (- \ infty, \ infty) $ вместо $ [0, \ infty) $.Я опускаю весь этот беспорядок.)
Точно такое же обсуждение применяется при нахождении p-значения, связанного с любым из других стандартных распределений в статистике. Еще раз, если данные распределены случайным образом (на этот раз в соответствии с каким-то другим распределением), то результирующие p-значения будут равномерно распределены в $ [0,1] $.
Как это применимо к нашим парным и непарным t-критериям? Дело в парном t-тесте, с выборками, выбранными независимо и случайным образом, как и в моем коде выше, значение t действительно следует t-распределению (с $ n-1 $ степенями свободы).Таким образом, p-значения, полученные в результате многократного повторения выбора X и Y, следуют равномерному распределению на $ [0,1] $. То же самое верно и для непарного t-критерия, хотя на этот раз t-распределение имеет $ 2 (n-1) $ степеней свободы. Тем не менее, полученные p-значения также имеют равномерное распределение на $ [0,1] $ в соответствии с общим аргументом, который я привел выше. Если приведенный выше код Питера применяется для определения p-значений, то мы получаем два различных метода построения случайной выборки из равномерного распределения на $ [0,1] $.Однако эти два ответа не являются независимыми.
р — Когда использовать парный t-тест
Поскольку этот вопрос был перенесен, я постараюсь свести жаргон к минимуму
Первая проблема для парного анализа заключается в том, что вам необходимо однозначное соответствие между отдельными точками данных в наборах акций и рынков. Таким образом, если отдельные цены на акции связаны с сопоставленным рыночным индексом, тогда данные подходят для парного теста.
Я предполагаю, что интересующий вас рыночный индекс включает в себя цену акций, поэтому при правильной выборке должна быть возможность получить соответствие один к одному, поскольку каждый рыночный индекс будет иметь определенное значение для соответствующей акции.(если это неверно, укажите более подробно в вопросе, что это за два образца)
Теперь нужно спросить, что именно вы хотите сравнить. Непарный тест проверяет, есть ли разница между средним индексом акций и средним рыночным индексом. Парный тест проверяет, отличается ли в среднем разница между фондовым и рыночным индексами от 0.
Парный тест полезен, когда у вас есть базовый тренд, который одновременно влияет на две переменные, так как спаривание совпадает с точками внутри этого тренда, оно сводит на нет его влияние.Без этой пары основные тенденции будут способствовать наблюдаемым вариациям в обоих наборах и увеличивать кажущийся уровень шума.
При отсутствии общей тенденции парные и непарные тесты должны дать одинаковый результат. При наличии основного тренда парный тест будет более чувствительным.
И, наконец, t-критерий — это проверка различия, а не равенства. В то время как низкое значение p, которое ниже вашего порога, является убедительным подтверждением существующей разницы, высокое значение p не является подтверждением равенства.Количество способов добиться того, чтобы тест упал, значительно превышает количество способов добиться его успеха, поэтому, если доказательство равенства — это то, что вам действительно нужно, вам нужен другой тест. Если это так, я бы порекомендовал сформулировать новый вопрос для сообщества, чтобы помочь нам понять, какая именно информация вам нужна из данных, чтобы мы могли помочь вам, как ее получить
Еще раз: парные и непарные t-тесты
Это интересный вопрос. Насколько я понимаю, вы действительно хотите знать, разумно ли использовать ваш метод сопряжения.Пункты 1, 2 и 4 из вашей интерпретации естественно следуют, если пункт 3 действителен, поэтому я не собираюсь их касаться.
Я начну с повторения вашей экспериментальной процедуры, насколько я понимаю, чтобы мы могли убедиться, что говорим об одном и том же.
Ваша процедура выглядит следующим образом:
- Определите меру P на парах мышей так, чтобы P (m1, m2) было маленьким, если m1 и m2 подобны, и большим в противном случае (для некоторых значений small и large).
- Пусть M будет набором из 20 случайно выбранных мышей.
- Определите M ‘как набор из 10 пар (m1, m2) $ \ in M $ таких, что $ \ sum_ {m \ in M’} P (m) $ минимизировано.
- Наугад, дайте лекарство A одному члену каждой пары $ M ‘$ и лекарство B другому члену, обращаясь с обоими участниками одинаково, в противном случае.
- Измерьте уровень холестерина $ C (m) $ каждой мыши.
- Выполните парный t-тест с нулевой гипотезой $ \ hat C (m_1) = \ hat C (m_2) $.
И, по сути, эксперт-критик возражает против вашего выбора $ P $ и, следовательно, против того, что вы использовали парный тест.Это правильно?
Если я правильно вас понял, тогда я думаю, что его критика разумна. Поскольку вы использовали парный тест, как указывал Эрик выше, неразумный метод сопряжения приведет к более или менее бессмысленному p-значению. Например, если ваш показатель спаривания был особенно глупым и был назначен аналогично обратному значению разницы в возрасте, тогда у мышей в паре были бы совершенно разные исходные уровни холестерина. С небольшой выборкой легко поверить, что небольшое p-значение может быть результатом случайной разницы в группе, назначенной каждому члену пары.В этом случае разумнее использовать непарный тест.
Тем не менее, если ваш метод разумен (например, вы проверили исходный уровень холестерина), я думаю, что это, вероятно, нормально. Таким образом, похоже, что реальная проблема заключается в том, можете ли вы оправдать свой выбор пар.
проверка гипотез — t-критерий для частично парных и частично непарных данных
Что ж, если бы вы знали дисперсии в непарных и парных (которые, как правило, были бы намного меньше), оптимальные веса для двух оценок разницы в средних для групп были бы иметь веса, обратно пропорциональные дисперсии индивидуальные оценки разницы в средних.
[Edit: оказывается, что когда расхождения оцениваются, это называется оценкой Graybill-Deal. Об этом было довольно много бумаг. Вот один]
Необходимость оценки дисперсии вызывает некоторые трудности (результирующее отношение оценок дисперсии равно F, и я думаю, что результирующие веса имеют бета-распределение, а итоговая статистика довольно сложна), но поскольку вы рассматриваете возможность начальной загрузки, это может меньше беспокоить.
Альтернативная возможность, что может быть лучше в некотором смысле (или, по крайней мере, немного более устойчивым к ненормальности, поскольку мы играем с отношениями дисперсии) с очень небольшой потерей эффективности при нормальном уровне, — это основание комбинированной оценки сдвига парных и непарных ранговых тестов — в каждом случае своего рода оценки Ходжеса-Лемана, в непарном случае на основе медиан попарных межвыборочных различий, а в парном случае — от медиан попарных средних пар разностей .Опять же, минимальная взвешенная линейная комбинация этих двух вариантов будет с весами, пропорциональными инверсии дисперсии. В этом случае я бы, вероятно, склонялся к перестановке (/ рандомизации), а не к начальной загрузке, но в зависимости от того, как вы реализуете свой бутстрап, они могут оказаться в одном и том же месте.
В любом случае вы можете захотеть робастизировать свою дисперсию / уменьшить коэффициент дисперсии. Правильно подобранный по весу — это хорошо, но вы очень мало потеряете эффективность при обычном весе, сделав его немного более прочным.—
Некоторые дополнительные мысли, которые я раньше не достаточно четко разобрал в голове:
Эта проблема имеет явное сходство с проблемой Беренса-Фишера, но еще сложнее.
Если бы мы зафиксировали веса, мы могли бы просто взломать в приближении типа Велча-Саттертуэйта; структура проблемы такая же.
Наша проблема заключается в том, что мы хотим оптимизировать веса, что фактически означает, что взвешивание не является фиксированным — и действительно имеет тенденцию максимизировать статистику (по крайней мере, приблизительно, а в большей степени в больших выборках, поскольку любой набор весов является случайной величиной, оценивающей тот же числитель, и мы пытаемся минимизировать знаменатель; эти два значения не являются независимыми).
Это, как я полагаю, ухудшит приближение хи-квадрат и почти наверняка повлияет на d.f. приближения еще дальше.
[Если эта проблема выполнима, то может оказаться хорошим практическим правилом, которое говорит: «Вы можете справиться почти так же хорошо, если будете использовать только парные данные в этих наборах обстоятельств, а только непарные в этих условиях». в других наборах условий и в остальном эта фиксированная схема веса обычно очень близка к оптимальной »- но я не буду задерживать дыхание, ожидая этого шанса.Такое правило принятия решения, несомненно, будет иметь некоторое влияние на истинное значение в каждом случае, но если бы этот эффект не был таким большим, такое практическое правило дало бы людям простой способ использовать существующее устаревшее программное обеспечение, поэтому было бы желательно попробуйте определить подобное правило для пользователей в такой ситуации.]
—
Редактировать: Примечание для себя — необходимо вернуться и подробно описать работу над тестами «перекрывающихся выборок», особенно t-тесты перекрывающихся выборок
—
Мне приходит в голову, что тест рандомизации должен работать нормально —
где данные объединены в пары, вы случайным образом переставляете метки групп внутри пар
, где данные не являются парными, но предполагается, что они имеют общее распределение (под нулем), вы переставляете групповые назначения
, теперь вы можете основывать веса для двух оценок сдвига на основе оценок относительной дисперсии ($ w_1 = 1 / (1+ \ frac {v_1} {v_2}) $), вычислять взвешенную оценку сдвига для каждой рандомизированной выборки и видеть, где выборка попадает в рандомизированное распределение.
(Добавлено намного позже)
Возможно релевантный документ:
Деррик Б., Расс Б., Тохер Д. и Уайт П. (2017),
«Тестовая статистика для сравнения средних значений для двух выборок, включающих как парные, так и независимые наблюдения»
Journal of Modern Applied Статистические методы , May, Vol. 16, № 1, 137–157.
DOI: 10.22237 / jmasm / 1493597280
http://digitalcommons.wayne.edu/cgi/viewcontent.cgi?article=2251&context=jmasm
Использование парного t-теста для сравнения супермаркетов Wegmans и Publix
Введение
В ожидании тилапии.
В ожидании тилапии могло бы стать названием нового инди-фильма об опасностях изменения климата. Но нет, я буквально ждал рыбу. Я обнаружил, что бесцельно смотрю на тилапию в моем местном супермаркете Publix (R). Свежая рыба находится за стеклянным экраном, который требует, чтобы сотрудник Publix извлек эту рыбу. Не поймите меня неправильно, я понимаю необходимость изолировать рыбу от покупателей. Было бы нежелательно, чтобы покупатели выжимали сырую рыбу и обращались с ней так же, как с апельсинами.Мое сожаление связано с тем, что я ждал несколько минут, а в поле зрения не было ни одного сотрудника Publix. В отделе морепродуктов не было персонала, и люди, которые отвечали за посещение морепродуктов, были хитроумно размещены за дверью с надписью «Publix Associates Only». Через несколько минут я сдался и решил вместо этого использовать курицу. Однако во время этого ожидания у меня появилась отличная идея для этой статьи.
Ожидая, я в тысячный раз оплакивал, что у нас нет Wegmans в Центральной Флориде.Если вам посчастливилось жить в непосредственной близости от супермаркетов Wegmans, значит, вы переживаете нирвану продуктовых магазинов. Я регулярно езжу в северные районы штата Нью-Йорк и привык к барам со свежими продуктами, китайскому шведскому столу, готовым овощам и основным блюдам, а также к ассортименту сыров, с которым может соперничать только Whole Foods. На мой взгляд, существует огромная разница в выборе и качестве между Publix и Wegmans. Но разве это дорого обходится? Взимает ли Wegmans дополнительную плату за еду, чтобы сделать покупки более комфортными? Так как у меня недавно возник вопрос о парном t-тесте, я решил использовать парный t-тест, чтобы определить, действительно ли Wegmans действительно дороже.
Парный t-тест
Парный t-тест можно использовать, когда ваши данные поступают в виде логических пар. Статистик может сказать, что вы «можете использовать парный t-тест, если у вас есть дополнительная информация о каждой выборке». Однако это определение бесполезно для среднего практикующего, поэтому позвольте мне уточнить. Классическое использование парного t-теста — это оценка до и после лечения. Например, измерьте артериальное давление у пациента А, дайте ему что-нибудь (лекарство, упражнения, тилапию), чтобы снизить артериальное давление, а затем снова измерьте артериальное давление у пациента А.Повторите для пациентов B, C, D,… В этом случае данные «До» и «После» сопоставляются пациентом.
| Показания систолического артериального давления | ||||
| Пациент | До | После | ||
| A | 170 | 165352 | 170 | 165 Пара ) |
| B | 110 | 112 | Пара № 2 (Пациент B до и после) | |
| C | 134 | 131 | Пара № 3 (Пациент C до и после) | |
Некоторые люди могут подумать, что Пациенту А удалось, поскольку его давление «после» ниже, чем «до».Не обязательно — вполне возможно, что давление «после» является результатом случайного изменения. То есть, мы ничего не могли сделать, и артериальное давление все равно снизилось бы на 5 пунктов. Подробнее об этом позже. Пример «До» и «После» — отличный способ познакомить с концепцией пар; однако существует гораздо больше применений парного t-теста, чем до и после тестирования. Как правило, вы можете использовать парный t-тест при соблюдении следующих условий.
- Точка данных из первой группы может быть спарена только с точкой данных из второй группы.Пример: 170 для пациента A «До» следует использовать только в паре с 165 для пациента A «После». Было бы нелогично сочетать предыдущую точку данных со 112 или 131, поскольку они были для разных пациентов.
- У вас должно быть одинаковое количество наблюдений для первой и второй групп. Если у вас есть 31 наблюдение для группы A и 30 наблюдений для группы B, этого недостаточно. Должно быть точно так же. Это должно иметь смысл, поскольку есть «пары»; если каждая группа — пара, как может быть разным количество баллов?
- Если данные были взяты в качестве случайных выборок, вы не сможете использовать парный t-тест, даже если существует фактор парности.Например, если мы дважды измерили артериальное давление пациентов (не давая им лекарства), то парный t-тест теряет смысл.
К чему такая суета по поводу парного t-теста?
Распространенный вопрос: почему мы должны использовать парный t-тест вместо более распространенного (непарного) t-теста. «Нормальный» двухвыборочный t-тест не делает предположение о парности, так какую же ценность мы получаем от сбора данных в «парах»? Статистический ответ состоит в том, что парный t-тест имеет большую мощность, чем обычный t-тест.Это технический способ сказать, что парный t-тест может помочь нам обнаружить различия, которые (непарный) t-тест может пропустить. Это особенно верно, если в данных есть выбросы или если набор данных сильно варьируется. Чтобы продемонстрировать это, я собираюсь использовать как парный t-тест, так и (непарный) t-тест, чтобы сравнить цены в Wegmans и Publix.
Если вы хотите узнать больше о (непарном) t-тесте, прочтите эту статью о Роджере Клеменсе и Барри Бондсе и предполагаемом употреблении наркотиков в бейсболе.
Шаг 1. Сбор данных
Моя гипотеза состоит в том, что Я плачу за продукты в Publix меньше, чем в Wegmans . В идеале я бы составил список всех продуктов, которые я покупаю в супермаркете, и сравнил бы цены на каждый товар в Wegmans и Publix. Хотя это теоретически возможно, на это потребуется нелепое количество времени. К счастью, я могу использовать случайную выборку и парный t-тест, чтобы ответить на вопрос за гораздо меньшее время.
Шаг 1 — случайный выбор 30 продуктов, которые я обычно покупаю в супермаркете.Важно составить эти «пары», и поэтому следует позаботиться о том, чтобы они были идентичными. Например, было бы плохой идеей сравнивать цену 1 галлона апельсинового сока в Wegmans с 1 квартой OJ в Publix (мы ожидаем, что одна кварта будет дешевле, чем один галлон). Вы можете загрузить полный список продуктов в книге Excel; Образцы 5 из 29 продуктов представлены в таблице ниже. Примечание: один из продуктов не был доступен ни в Wegmans, ни в Publix, поэтому я удалил этот элемент из списка.
Цена первых пяти продуктов из 29 составляет в долларах США
| Продукт | Цена Wegmans | Цена Publix | 1,89 | 3,55 |
| Йогурт Activa, простой, большой | 2,69 | 2,39 | |
| яйца, большие, сорт A, дюжина | 1.29 | 2,69 | |
| Арахисовое масло сливочное Jif, 40 унций. | 4,39 | 5,87 | |
| Diet Coke, 12 пакетов | 3,33 | 4,99 |
Примечание: эти цены не вымышленные, они действительны с 6 марта 2011 года. Wegmans в Вебстере, штат Нью-Йорк, а затем 8 марта 2011 г. из Publix в Уиндермире, штат Флорида.
Шаг 2: Парный t-тест
Как и все проверки гипотез, парный t-тест начинается с двух гипотез, нулевой и альтернативной.В случае парного t-теста они основаны на различии в каждой паре. В частности…
Для нашего конкретного теста мы заменим общие термины «Группа A» и «Группа B» фактическими группами, такими как Wegmans Price и Publix Price.
Разница в «средней разнице» — это дельта между каждой парой. Наверное, это легче понять на примере. В таблице ниже разница для каждой пары указана в новом столбце под названием «Разница».Для обезжиренного молока разница составляет 1,89–3,55 доллара, что составляет -1,66 доллара. Этот расчет продолжается для всех 29 строк. Затем рассчитывается средняя разница для всех 29 пар. В таблице ниже показаны только первые 5 пар; щелкните здесь, чтобы загрузить полный набор данных в файле Цены Publix и Wegmans для парного t-Test.xls.
| Продукт | Цена Wegmans | Цена Publix | Разница | ||||||
| обезжиренного молока89 | 3,55 | -1,66 | |||||||
| Йогурт Activa, простой, крупный | 2,69 | 2,39 | 0,3 | яйца большие 1,2 | 2,69 | -1,4 | |||
| Арахисовое масло сливочное Jif, 40 унций. | 4,39 | 5,87 | -1,48 | ||||||
| Diet Coke, 12 пакетов | 3.33 | 4,99 | -1,66 | ||||||
| (еще 24 продуктов…) | |||||||||
| -.809 |
Многие люди остановятся на этом и заявят, что Wegmans дешевле, поскольку средняя разница отрицательная (помните, что разница Wegmans — Publix, поэтому отрицательная разница означает, что Wegmans дешевле).Это был бы плохой вывод. Причина, по которой мы не можем сразу прийти к выводу, что Wegmans дешевле (, это плохое время для вашего счастливого места ), заключается в том, что у нас есть выборка , а не вся совокупность . Если бы мне пришлось сравнивать стоимость моих покупок в супермаркете на протяжении всей моей жизни в Wegmans и Publix, то мне не пришлось бы беспокоиться обо всех этих проверках гипотез. Однако это выходит за рамки возможностей. Поэтому я вынужден использовать образец, а образец имеет ошибку .
Один мудрец однажды сказал: «Если даны два числа, одно будет больше». Конечно, существует очень небольшая вероятность того, что средняя разница окажется равной нулю, но более вероятно, что она будет в пользу Wegmans или Publix. Что, если бы разница составила 0,01 (один пенни) в пользу Wegmans? Не могли бы вы сказать, что покупка в Wegmans в долгосрочной перспективе сэкономит вам деньги по сравнению с Publix? Возможно, Wegmans только что получил большую партию яиц и сделал скидку на их перевозку, пока они не испортились.Возможно, если вы выберете другие 29 продуктов, разница составит 0,01 в пользу Publix. Надеюсь, вы видите, что из-за очень небольшой разницы наша уверенность в том, что Wegmans действительно дешевле, может быть ошибочной.
Что, если бы средняя разница по 29 товарам составляла 100 долларов (я понимаю, что это абсурд; я подчеркиваю). Для этого цена Wegmans на яйца составит 1,89 доллара, а цена Publix — 101,89 доллара (в среднем). С такой большой разницей мы можем сделать вывод, что Wegmans дешевле с очень малой вероятностью ошибки.
Итоги на данный момент…
Если средняя разница составляет -0,01 доллара, мы знаем, что у нас есть большой шанс сделать ошибку, если мы сделаем вывод, что Wegmans дешевле.
Если средняя разница составляет -100 долларов, мы знаем, что у нас мало шансов сделать ошибку, если мы сделаем вывод, что Wegmans дешевле.
Было бы неплохо, если бы мы могли рассчитать вероятность ошибки на основе разницы (и размера выборки). Здесь на помощь приходит парный t-тест.Он вычисляет «значение p», которое и есть вероятность ошибки. Говоря более формально (и я собираюсь перейти к статистике, чтобы не получить никаких неприятных граммов от встревоженных статистиков), мы можем рассчитать вероятность ошибки, если мы сделаем вывод H 1 или альтернативную гипотезу. Если вспомнить, что наша таблица гипотез выглядит так…
… альтернативная гипотеза на простом английском языке — «цена Wegmans и Publix для населения отличается».(Примечание для встревоженных статистиков: я расскажу об односторонних тестах буквально через секунду; сохраняйте спокойствие.) Еще раз помните, что мы взяли образец из 29 продуктов из моего списка покупок. А теперь мы подошли к ключевому моменту проверки гипотез (иначе говоря, еще одно плохое время, чтобы оказаться в вашем счастливом месте).
Проверка гипотез позволяет нам сделать выводы о популяции , используя выборку . Для этого теста совокупность — это каждый продукт, который я куплю в супермаркете в течение своей жизни.Образец — это 29 продуктов, которые я произвольно выбрал из своего списка покупок. Получить генеральную совокупность практически всегда невозможно, что делает использование выборки желательным. Однако при использовании образца возникает ошибка . Сначала мы решаем, каков наш допуск к риску (вероятность ошибки 5%, 10% и т. Д.), А затем с помощью проверки правильной гипотезы вычисляем фактическое количество ошибки.
Довольно теории, давайте займемся математикой. Используя функцию парного t-теста Quantum XL, я рассчитал парный t-тест с результатами, приведенными ниже.
Quantum XL разбивает анализ на три части: проверенная гипотеза, результаты и статистика набора данных. Статистика набора данных — это просто полезная информация, но проверенные гипотезы и результаты заслуживают особого внимания.
Гипотеза проверена
В разделе Проверенная гипотеза повторяется гипотеза в том случае, если вы не помните все подробности из этой статьи. Если ваши наборы данных включают заголовки (например, слова «Wegmans» и «Publix»), тогда гипотеза будет сформулирована в этих терминах.Я настоятельно рекомендую использовать заголовки, так как это упрощает дальнейшую интерпретацию. Еще раз, нулевая гипотеза состоит в том, что средняя разность равна нулю; альтернатива — средняя разница не равна нулю.
Результаты
В разделе результатов есть «ответ» или наше значение P, наша вероятность сделать ошибку, если мы придем к выводу, что разница в цене не равна нулю. В нашем случае значение P настолько близко к нулю, что Excel округляет его до нуля.
На самом деле вероятность ошибки никогда не может быть равна нулю; Excel округляет результаты.Я переформатировал результаты и отобразил значение P на большее количество цифр с результатом, приведенным ниже. Если мы сделаем вывод, что цены для населения разные, то у нас будет только 0,0000153 (или 0,00153%) шанс ошибиться. Для сравнения: у нас есть 15 шансов из миллиона сделать ошибку. Примечание. Значение T немного странно, и, если вы не хотите разбираться в математике, лежащей в основе этого теста, нам не нужно его использовать.
Ниже значения P приведена вспомогательная информация. Поскольку мы знаем, что разница, скорее всего, не равна нулю, тогда что это такое? Что ж, в этом случае мы можем быть на 95% уверены, что разница составляет 1 доллар.13 и -. 49, с расчетной разницей, равной -0,81 доллара. Или, проще говоря, Wegmans дешевле на 0,49–1,13 доллара.
Как мне указать результаты?
Если вы помните, это началось, когда я ждал Tilapia в моем локальном Publix. Я предположил, что Wegmans должны брать больше за свой превосходный опыт покупок (на мой взгляд). Я обосновал свою гипотезу, а затем собрал образец. Боковое примечание: я чуть не упал со стула, когда увидел, что Wegmans дешевле, чем Publix, на эти 29 позиций.Однако я могу продолжить свой анализ, чтобы определить, является ли это случайной вариацией или реальной разницей. Используя образец, я вычислил значение P на уровне 0,0000153. Здесь я должен быть осторожен с тем, что это означает. Итак, давайте рассмотрим несколько вариантов того, как это заявить.
Метод 1. Жесткая статистика нацистского метода. Если вы читаете медицинские журналы для развлечения, вы можете увидеть похожие утверждения.
Я решаю отвергнуть нулевую гипотезу и сделать вывод о альтернативной.Вероятность того, что это ошибка, составляет 0,00153%, что ниже моего ранее заявленного порога риска в 5%.
Метод 2: более удобный, но все же правильный метод
Основываясь на нашей выборке из 29 продуктов, мы можем сделать вывод, что цены Wegmans и Publix отличаются с вероятностью ошибки, равной 0,000015.
Метод 3: Самый простой для понимания (осторожность: может вызвать беспокойство у статистиков)
На основе моей выборки из 29 продуктов мне 99 лет.99846% уверены, что цены у Wegmans и Publix разные.
Причина, по которой метод 3 вызывает паузу, связана с заменой «вероятность ошибки» на «процент достоверности». Лично я использую этот метод, так как эта интерпретация может коснуться большего числа людей, чем две другие.
Напоследок я должен отметить распространенную ошибку, что неверно, и не только в скандальной статистике нацистов.
Метод 4: общепринято, но неверно
Вероятность совпадения средних составляет 0,00153%.
То, что я только что изменил, было тонким, поэтому позвольте мне убедиться, что вы это уловили. Вместо выражения процента ошибки как «не равно» (что является H 1 или альтернативной гипотезой) я переключился на «равно», что является H 0 или нулевой гипотезой. Мы не должны этого делать. Одно дело — вычислить вероятность того, что два средних значения не равны, но мы не можем говорить о равенстве. Почему? Что ж, это довольно сложная концепция и одна из самых запутанных частей проверки гипотез. Мы можем найти доказательства того, что средства ненормальны, и выразить уверенность в том, что средства ненормальны, но это не то же самое, что свидетельство того, что средства являются нормальными.
Сравнение парного t-теста с «нормальным» или непарным t-тестом
Quantum XL также включает в себя нормальный или непарный t-тест. Большинство программ обычно называют это двухвыборочным t-тестом или просто t-тестом (если не упоминается спаривание, предполагается, что он непарный). Если я проведу непарный t-тест для этого набора данных, результаты будут ниже.
Обратите внимание, что значение P намного больше, чем в парном t-тесте. Если я сделаю вывод, что они разные, то вероятность ошибки составляет 32,56% (1 из 3).Для большинства экспериментаторов это слишком большая вероятность ошибки, и они заявят, что не смогли найти разницу в средствах. Обратите внимание, что выводы противоположны в зависимости от того, какой тест я выполняю.
Если я использую парный t-тест, я прихожу к выводу, что средние цены разные.
Если я использую (непарный) t-тест, мне не удается найти разницу в средних значениях.
Почему результаты t-теста так сильно различаются? Я собираюсь на секунду окунуться в какую-нибудь увлекательную математическую речь. Если вам это неинтересно или вы не готовы к этому, просто помните, что вам следует использовать парный t-тест, если ваши данные попадают в пары, и переходите к следующему разделу.Если вам нравятся странные вещи, читайте дальше. Для этого набора данных ответ заключается в вариации. Поскольку цены на отдельные продукты сильно различаются, это проявляется в t-тесте как шум. T-тест основан на значении T, которое по сути является отношением сигнал / шум. Более формально математика для t-теста приведена ниже.
По мере увеличения шума значение T будет уменьшаться. В результате получается меньшее значение Т и большее значение Р. Для получения дополнительной информации о математике, лежащей в основе (непарного) t-критерия, он полностью объяснен в статье «Расчет вероятности типа I на примере набора данных Роджера Клеменса».Когда мы используем парный t-тест, разница между ценами на товары устраняется, что значительно снижает уровень шума. Различия сравниваются, различия между продуктами не рассматриваются.
Односторонний тест
Ранее в этой статье я указывал, что я хотел бы успокоить встревоженных статистиков нацистов односторонним обсуждением теста. Концепция одностороннего теста действительно довольно тривиальна. Вместо того, чтобы нулевая гипотеза была равенством, оно меньше или равно некоторому числу, обычно нулю.Ниже приводится формальное определение двустороннего и одностороннего теста, основные отличия которого выделены жирным шрифтом.
Двусторонний тест
Односторонний метод тестирования 1 (является менее дорогим для Publix)
Односторонний метод тестирования 2 (менее затратен Wegmans)
В то время как двусторонний тест призван ответить на вопрос «отличаются ли цены», односторонний тест ближе к нашему первоначальному запросу «Publix дешевле?».Использование одностороннего теста неоднозначно, но позвольте мне объяснить это в конце.
Проверки гипотез Quantum XL включают варианты для проведения одностороннего или двустороннего теста. Если я провожу тест для исходной гипотезы (он же «Дешевле ли Publix»), то я бы выполнил односторонний тестовый метод 1. Формальное изложение гипотезы и результат приведены ниже.
Односторонний метод тестирования 1 (является ли Publix менее дорогим)
Значение P равно.99999233, а это означает, что если мы придем к выводу, что Publix дешевле, то вероятность ошибки составляет 99,9999233%. Это не лучший вариант. Фактически, проведение этого теста было безумием, поскольку данные выборки показывают ценовое преимущество Wegmans. Итак, давайте посмотрим на односторонний метод 2 (дешевле ли Вегманс).
Односторонний метод тестирования 2 (менее дорогой вариант Вегманса)
Это больше похоже на это. Наше значение P указывает на то, что если мы придем к выводу, что Wegmans дешевле, то у нас будет.000767% шанс ошибиться. Разве вы не хотите, чтобы у вас были такие шансы в Вегасе?
А теперь полемика. Односторонний (иногда называемый односторонним) тест для большинства тестов гипотез возвращает значение P, которое вдвое меньше, чем у двустороннего теста. В этом примере двусторонний тест привел к значению P = .0000153; односторонняя составляла ровно половину этого значения. Так почему это вызывает беспокойство? Многие люди проводят проверку своих гипотез таким образом…
- Соберите данные о Wegmans vs.Publix.
- Рассчитайте среднюю разницу и обратите внимание, что для образца Wegmans дешевле.
- Поза Гипотеза «Является ли популяция цен в Wegmans дешевле, чем Publix?»
- Используйте парный t-тест Quantum XL для определения значения Р.
- Если значение P меньше 0,05, то можно сделать вывод, что Wegmans дешевле; если нет, то сделайте вывод, что вы не знаете.
Этот поток кажется нормальным, но на самом деле это не так. Причина в том, что вы просмотрели данные на втором этапе, прежде чем сформировали свою гипотезу на третьем этапе.Это своего рода статистическая проблема, но если вы задумаетесь, вы всегда можете уменьшить значение P вдвое, так как вы всегда будете знать, какая выборка имеет меньшую среднюю разницу .
Правильный поток выглядит примерно так…
- Поза Гипотеза «Является ли Publix дешевле, чем Wegmans» и установить значение критерия для принятия альтернативы (обычно 0,05).
- Соберите образцы данных.
- Используйте парный t-тест Quantum XL для определения значения Р.
- Если значение P меньше, чем.05, затем заключаем, что Publix дешевле; если нет, то сделайте вывод, что у вас недостаточно доказательств.
Обратите внимание, что мы сначала сформировали гипотезу. Причудливая фраза «установите значение критерия» на первом шаге просто означает, что вы решаете, прежде чем запускать тест, на какой риск вы готовы пойти. Наиболее частое значение — 0,05. Как Вы этим пользуетесь? Допустим, вы прошли тест, и значение P оказалось меньше 0,05; тогда вам следует принять альтернативную гипотезу. Однако, если он окажется больше, чем.05, то вы должны отклонить альтернативную гипотезу и принять нулевое значение. Это означает, что если он окажется равным 0,05001, вам следует отклонить альтернативный вариант. Большинство людей так поступают? Откровенно говоря, нет (даже у жестких статистиков).
Заключительное обсуждение
Парный t-тест — отличный инструмент, когда его использование уместно. Если данные логически сгруппированы в пары, парный t-тест более эффективен, чем (непарный) t-тест.
Исходя из моей выборки, моя первоначальная гипотеза была неверной.Publix не дешевле. Наоборот, на самом деле. Что касается продуктов, которые я покупаю, я уверен, что Wegmans дешевле. Я сейчас нахожусь в некоторой головоломке: как Wegmans может позволить себе предоставлять гораздо более качественный опыт (опять же, на мой взгляд) по сравнению с Publix? У меня нет на это ответа, но я планирую спросить Вегманса в следующий раз, когда буду там.
Раскрытие информации и отказ от ответственности
Я не аффилирован ни с Wegmans, ни с компанией Publix. Мне не платили ни одна из сторон, и я никогда не работал ни с одной из компаний.
Этот анализ касался моих покупательских привычек. Я не выбрал 30 товаров наугад, я выбрал 30 товаров наугад из моего списка покупок . Почему? Моей целью было узнать, выиграю ли я от покупок в Wegmans (а не в обычном потребителе). Другой образец из другого списка покупок может дать другой ответ.
Согласно Википедии, Wegmans находится в частной собственности, генеральным директором является Дэнни Вегман. Дэнни, если вы читаете это, пожалуйста, я умоляю вас, расширите свою сеть супермаркетов до Центральной Флориды, я устал ждать тилапии с завышенной ценой.
Я собирался разместить несколько картинок со статьей; однако отдел по работе с потребителями Wegmans не разрешил делать снимки в магазине. Это единственная головная боль в большинстве хороших опытов с Wegmans. Они не создают бомбардировщики-невидимки; А что насчет сыра и продуктовых дисплеев может быть секретом? Возможно, их тилапии работают с ЦРУ. Отдел по делам потребителей Wegmans также отказался от интервью и комментариев.
Исправления и дополнения
22 марта 2011 г. — Читатель заметил, что на вывеске на двери рядом с отделом морепродуктов написано «Только для Publix Associates», а не «Только для сотрудников».
22 марта 2011 г.



 Он только мягкий. По своему звучанию он самый близкий из сонорных звуков к гласным звукам, особенно близок к – [и]. Иногда его даже называют «и – краткое»
Он только мягкий. По своему звучанию он самый близкий из сонорных звуков к гласным звукам, особенно близок к – [и]. Иногда его даже называют «и – краткое»



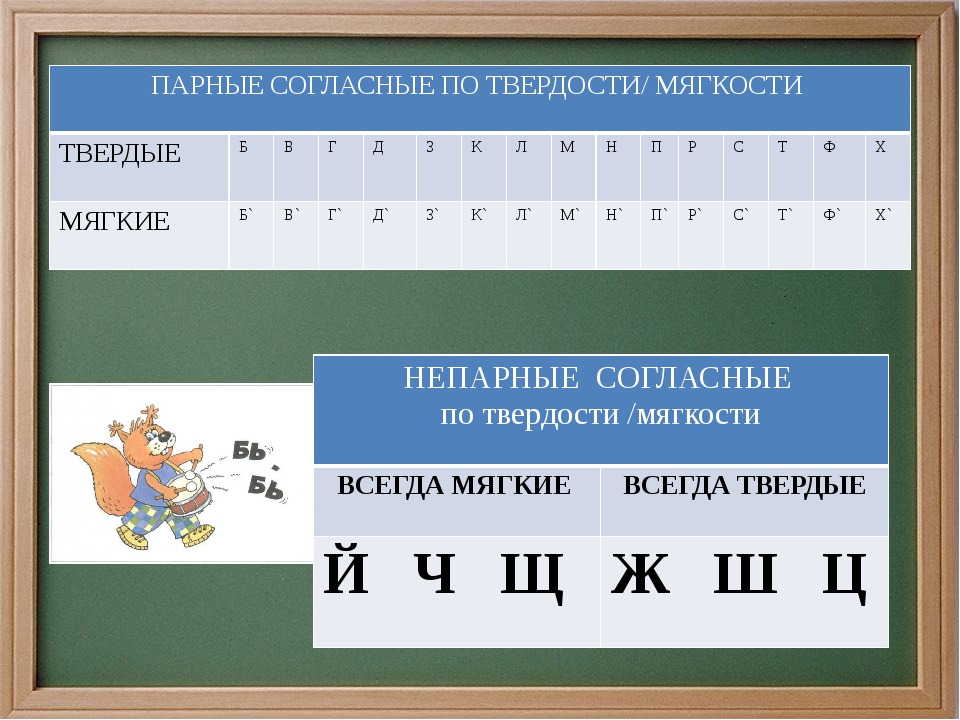
 Поёт [пай’о т ] – 4 буквы, 5 звуков.
Поёт [пай’о т ] – 4 буквы, 5 звуков.