Таблица умножения до 20 и до 100
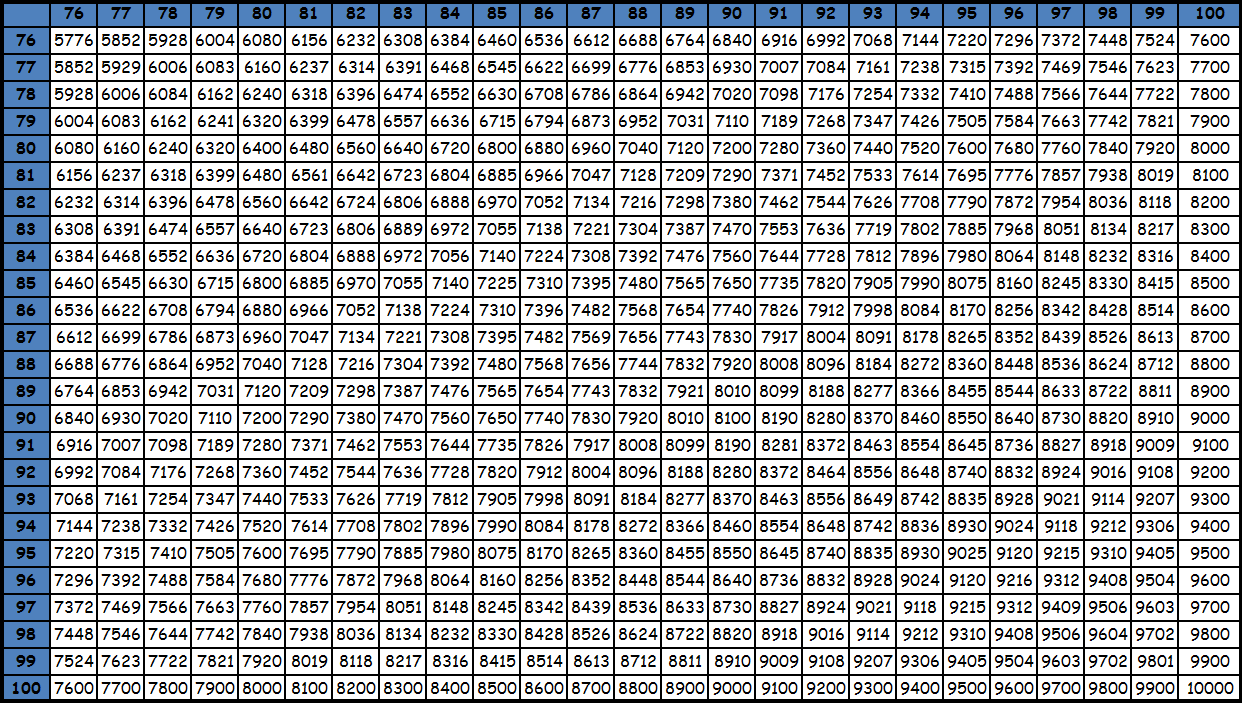
Умножение чисел с большим количеством знаков является довольно трудоемким процессом. Зная таблицу умножения до 10 можно считать в столбик. Подробно об умножении в столбик написано на отдельной странице. Как еще можно облегчить эту задачу? Если часто приходится прибегать к одним и тем же операциям с числами до 100, то иногда может оказаться, что намного удобнее пользоваться таблицей с уже подсчитанными значениями. Легче всего встретить таблицу со значениями до 20. Выглядит она так: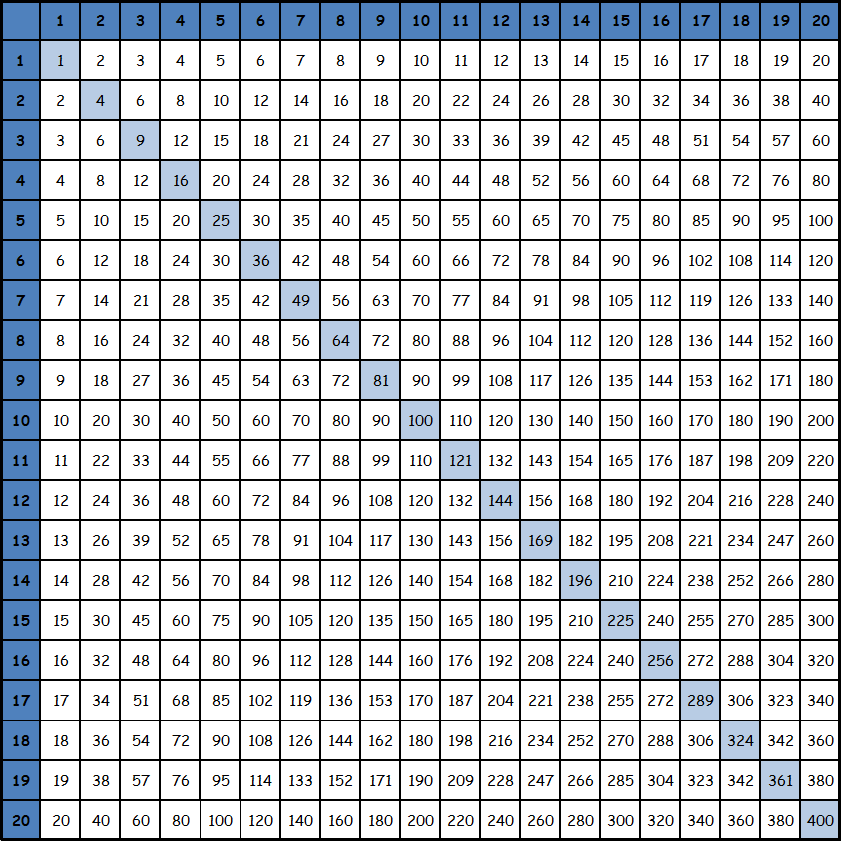
Принцип умножения по этой таблице такой же, как и по таблице Пифагора до 10. То есть, находим нужную строку, затем нужный столбец. Для такой таблицы тоже справедлива симметрия. То есть для заучивания достаточно рассмотреть только значения выше диагонали или значения ниже диагонали. Эта же таблица существует в виде записи равенств.
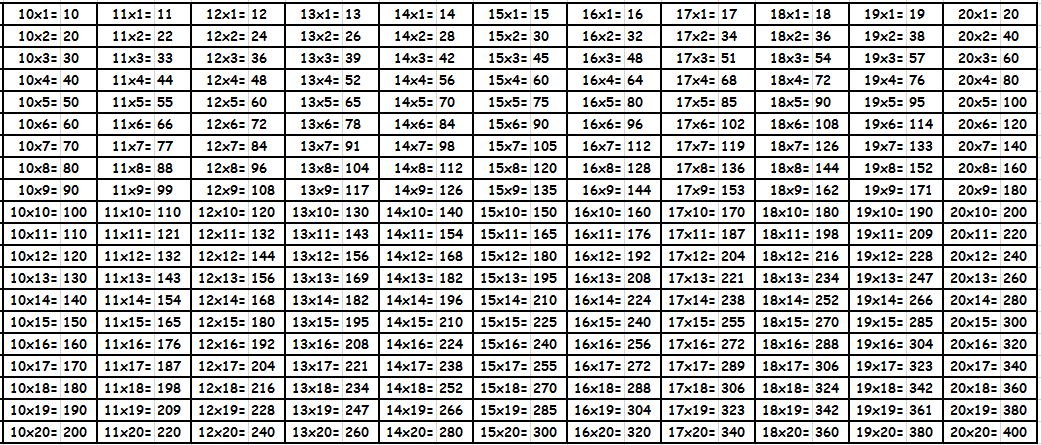
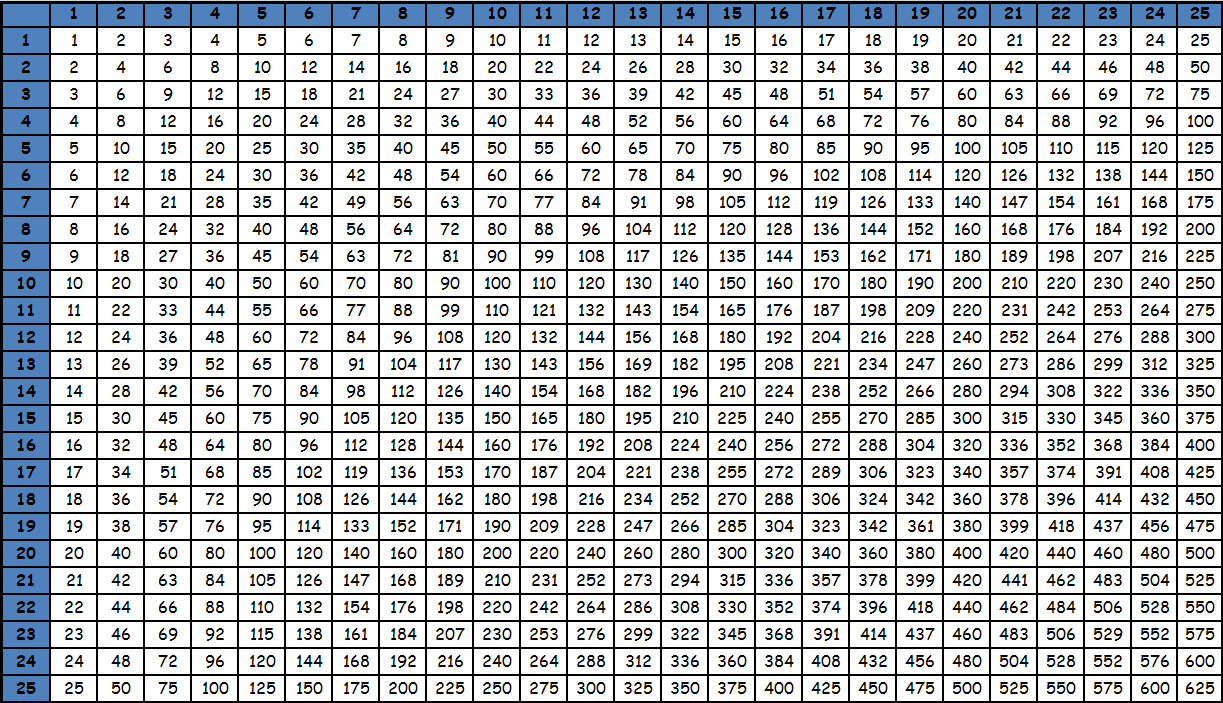
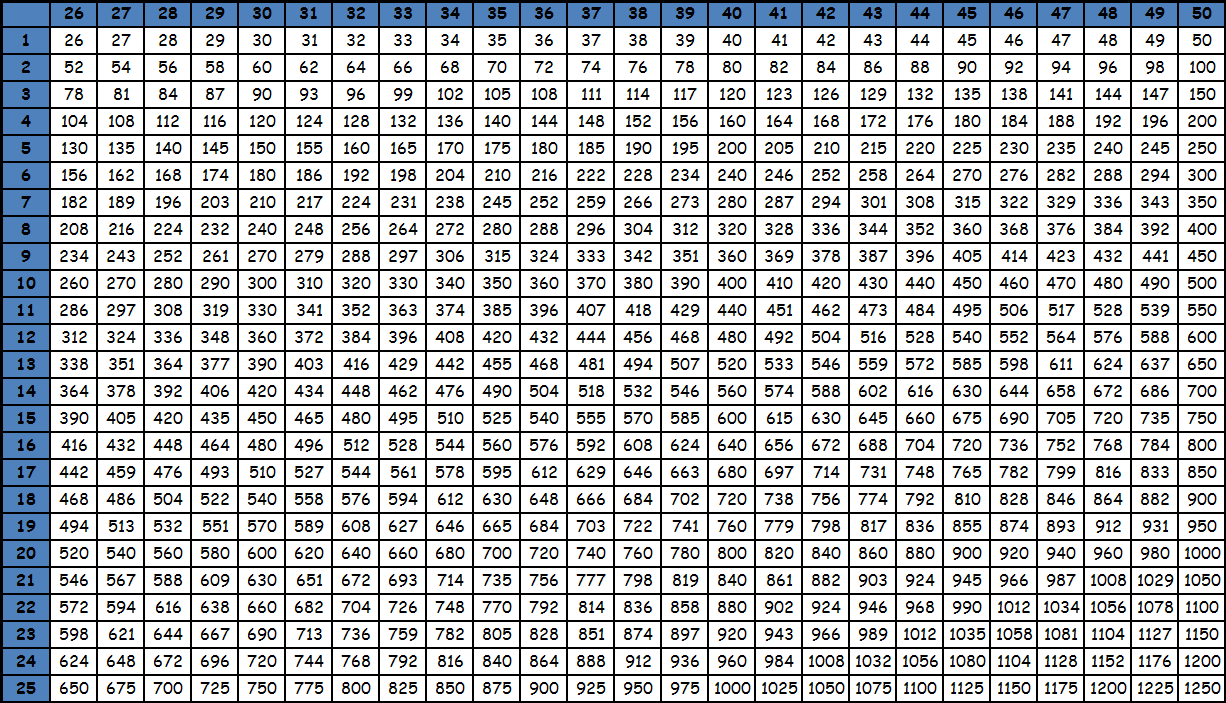
Умножение до 100 в виде таблицы равенств из-за ее громоздкости, как правило, не представляют. Пользуются фрагментами большой квадратной таблицы с соответствующими значениями. Принцип поиска по этим таблицам точно такой же: число в ячейке на пересечении столбца и строки с нужными множителями — есть искомое значение. При необходимости из этих фрагментов составляется одна большая таблица умножения до 100. Приведем пример. Необходимо умножить 95 на 87. Видим, что оба этих значения есть в последней таблице. Находим в столбце число 95, в строке число 87. Смотрим, что на пересечении их находится значение 8265. Таким образом, 95х87= 8265. Подобные таблицы оказываются под рукой нечасто, поэтому для таких вычислений на практике люди чаще пользуются калькуляторами. Тем более, калькуляторы сейчас есть в каждом смартфоне. Кроме того существуют специальные способы счета, которые позволяют в том числе и выполнять умножение двузначных чисел, например ментальная арифметика и счет с помощью пальцев. О них мы напишем в специальном разделе. Тем не менее таблицы с уже посчитанными значениями приведены ниже для ознакомления. Также при желании их можно скачать и распечатать, для этого нужно использовать ссылку или же нажать правую кнопку мышки над картинкой и выбрать вариант «сохранить картинку как».
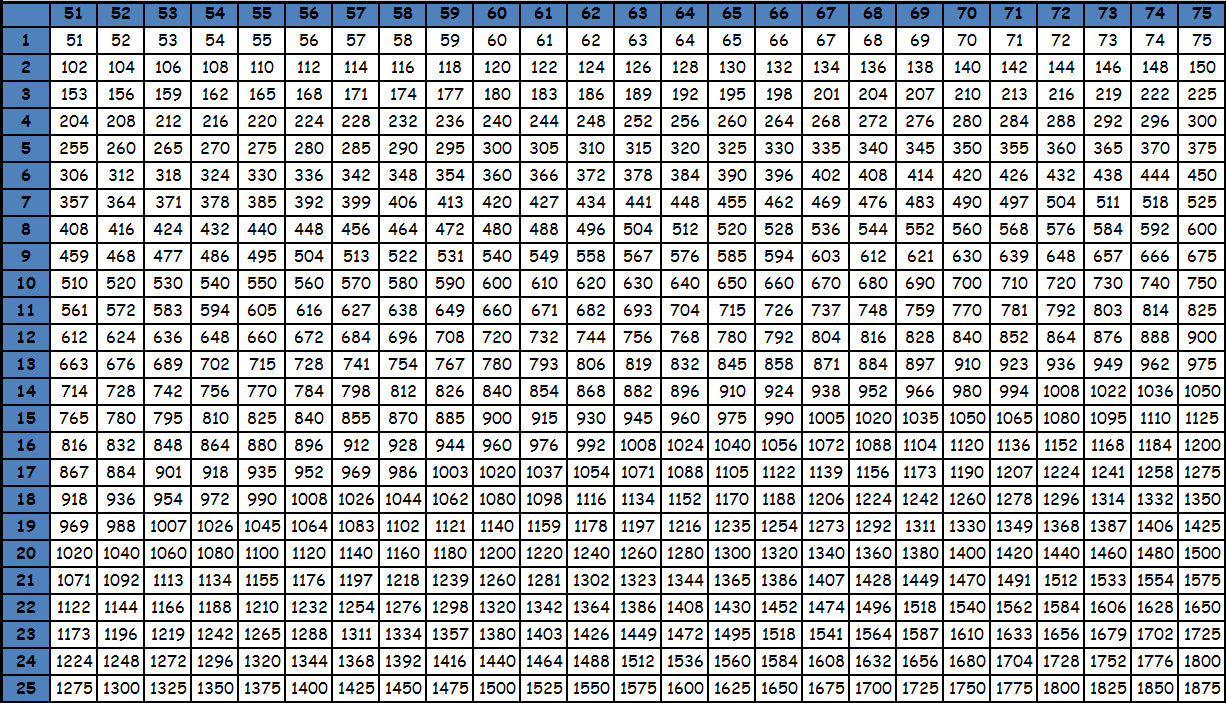
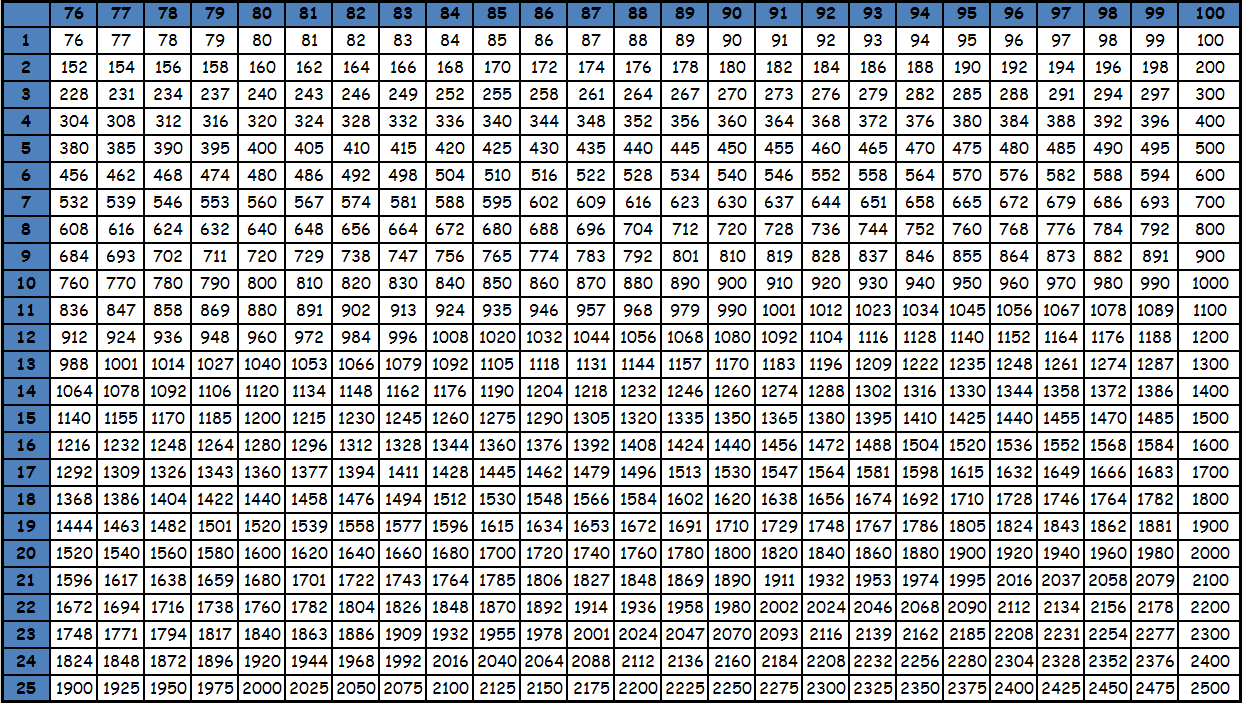
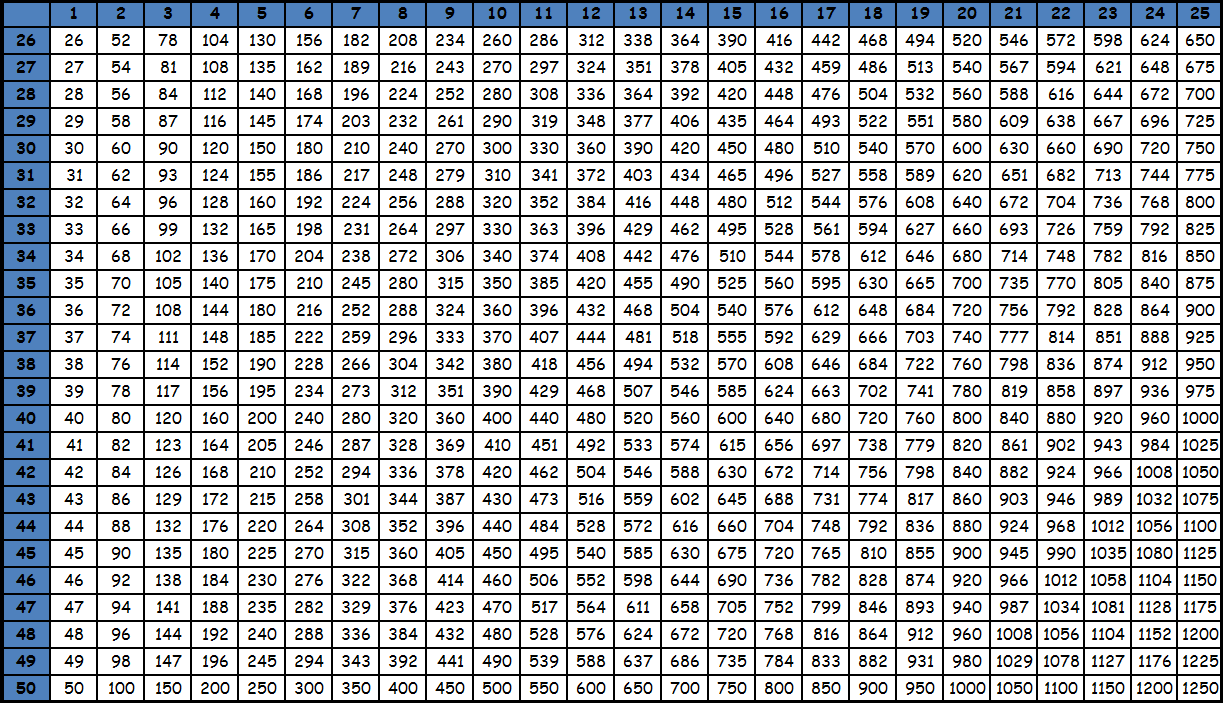
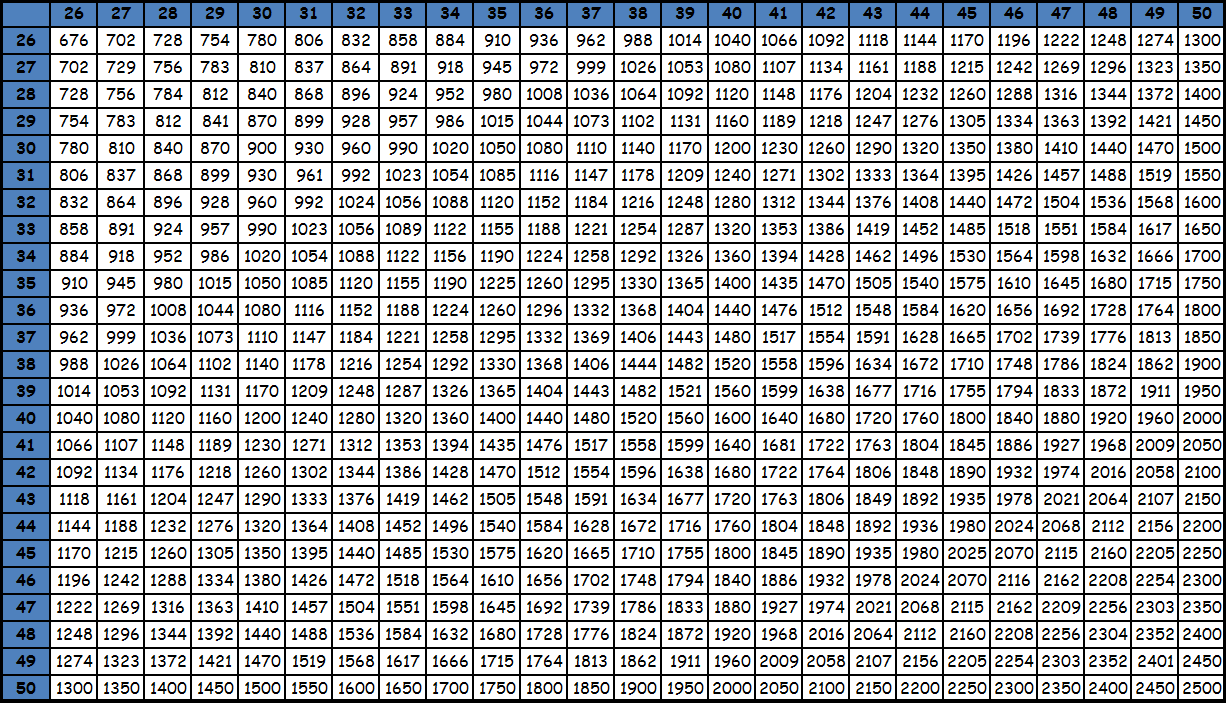


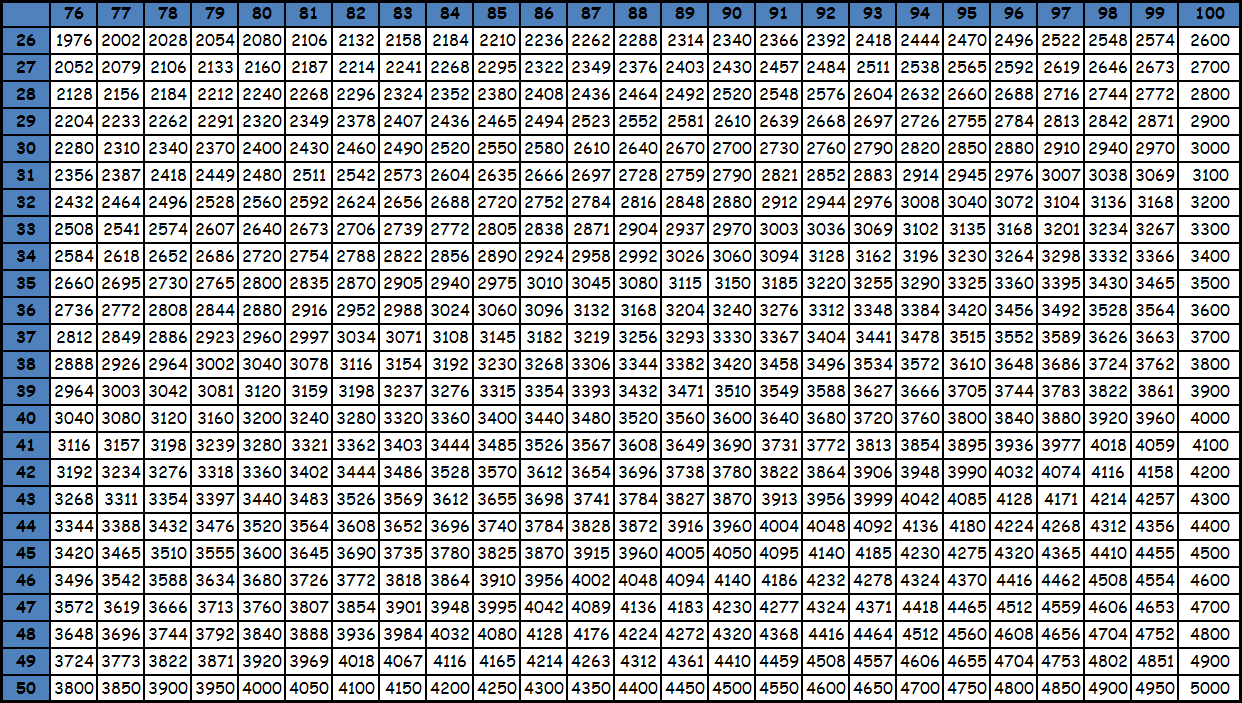
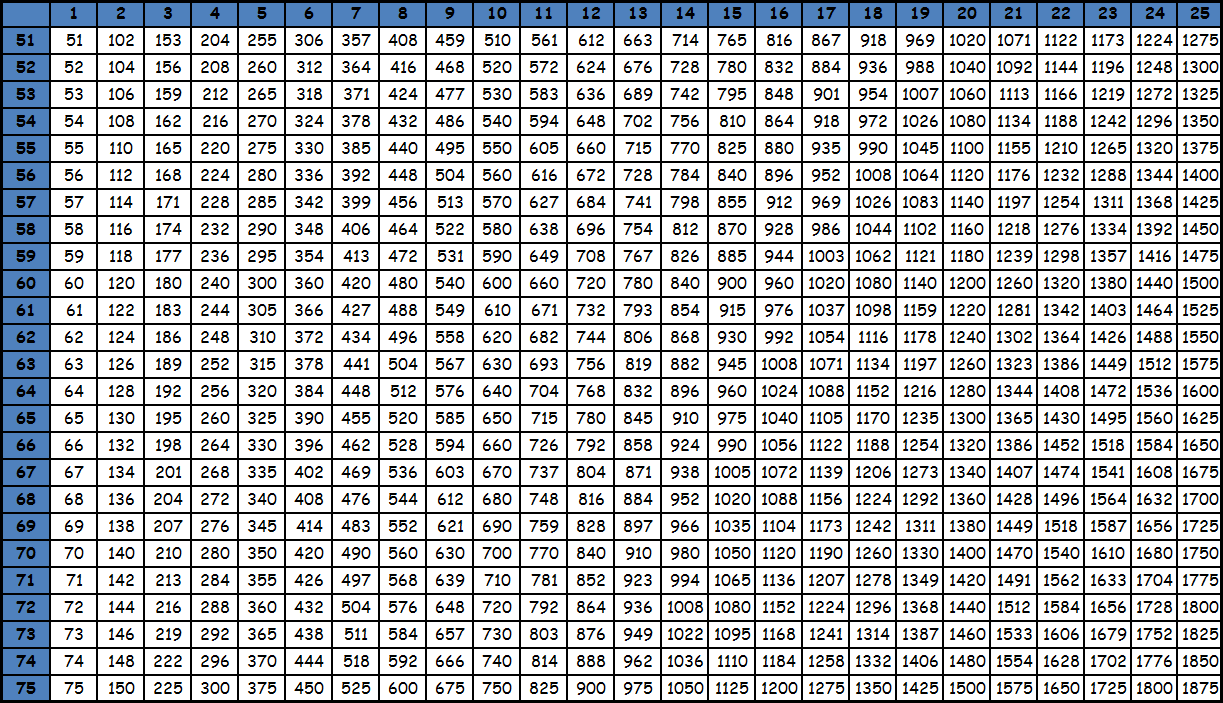
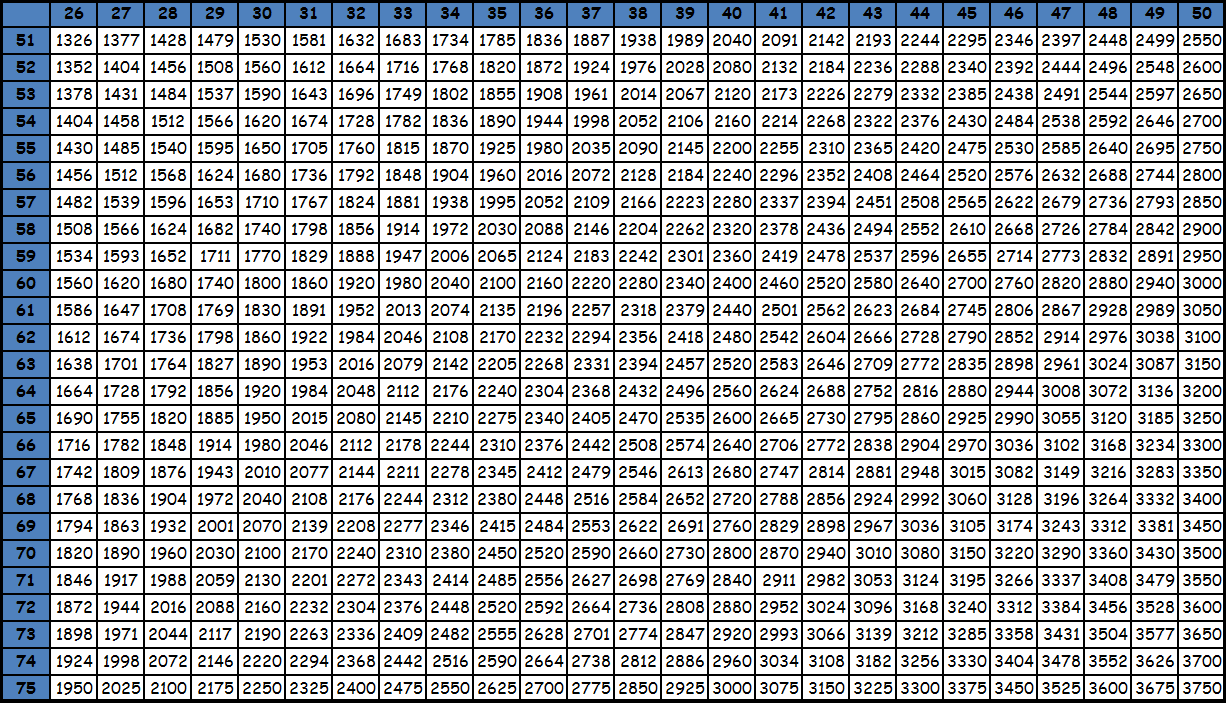
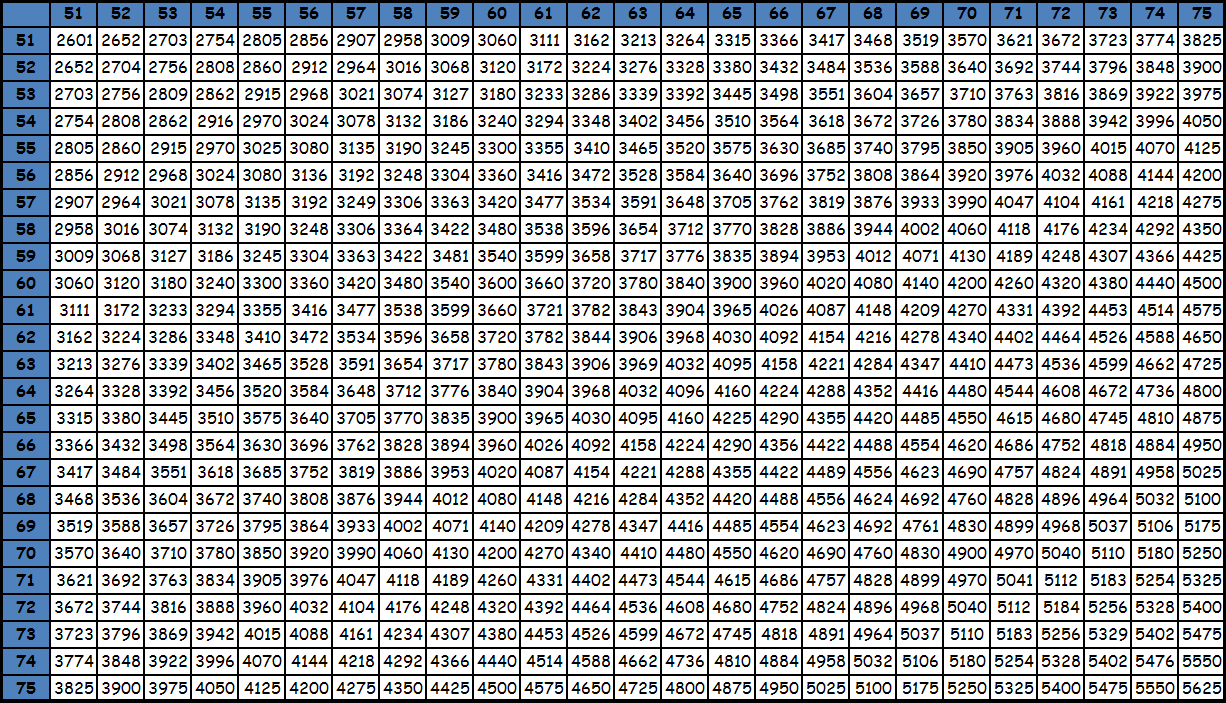
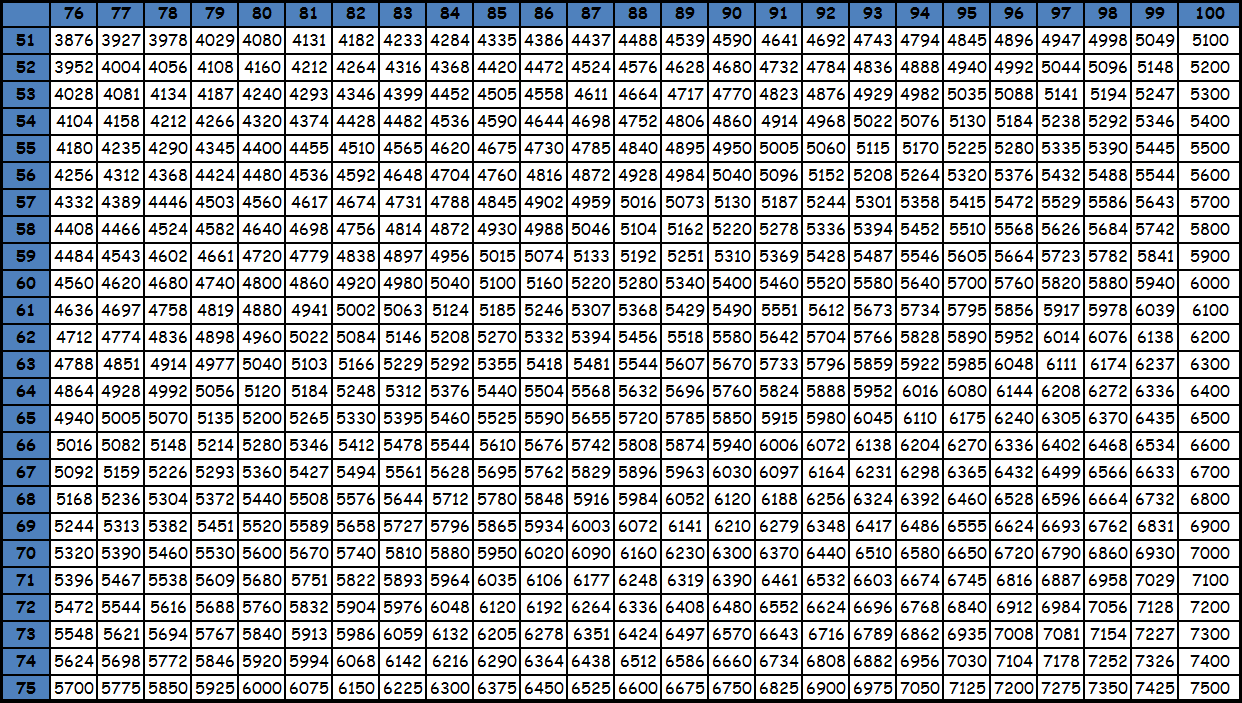
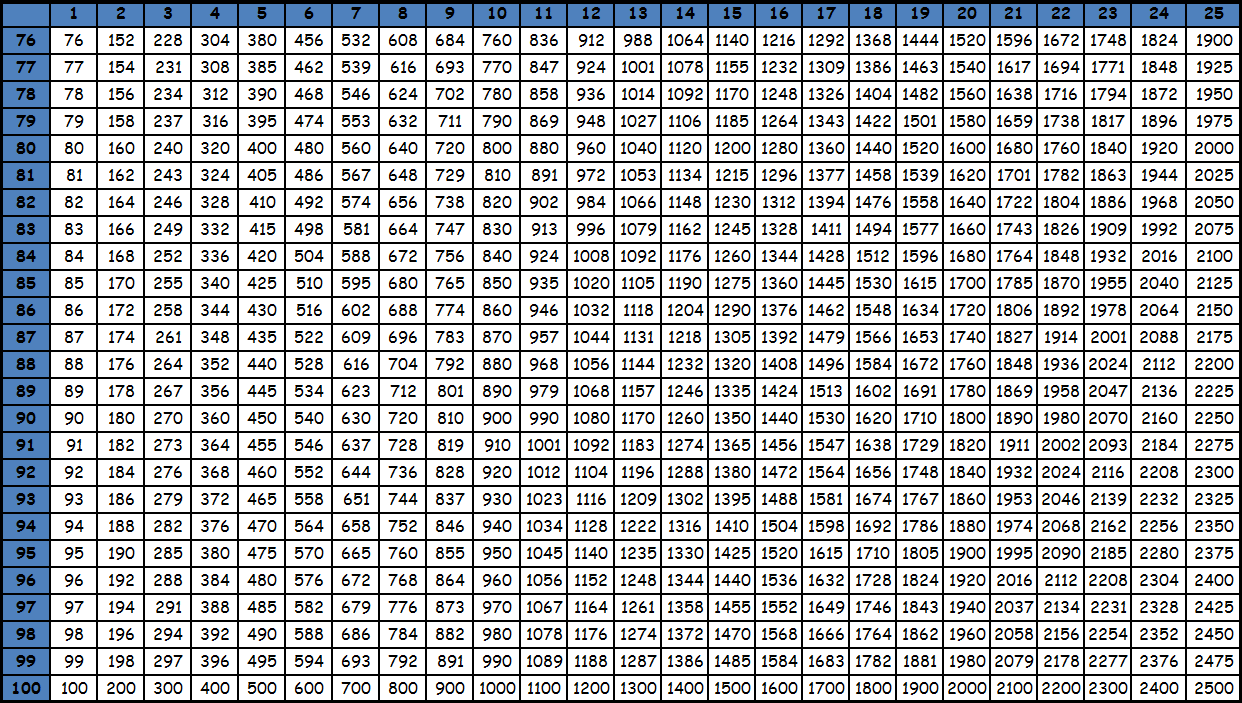
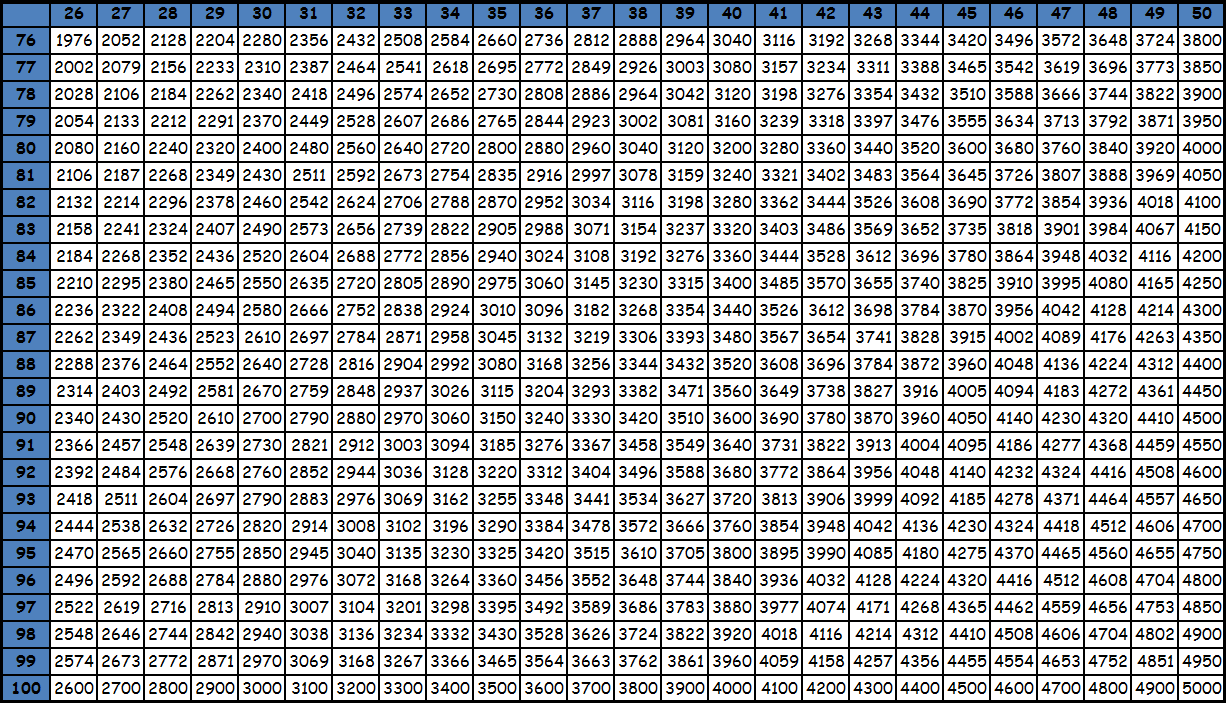
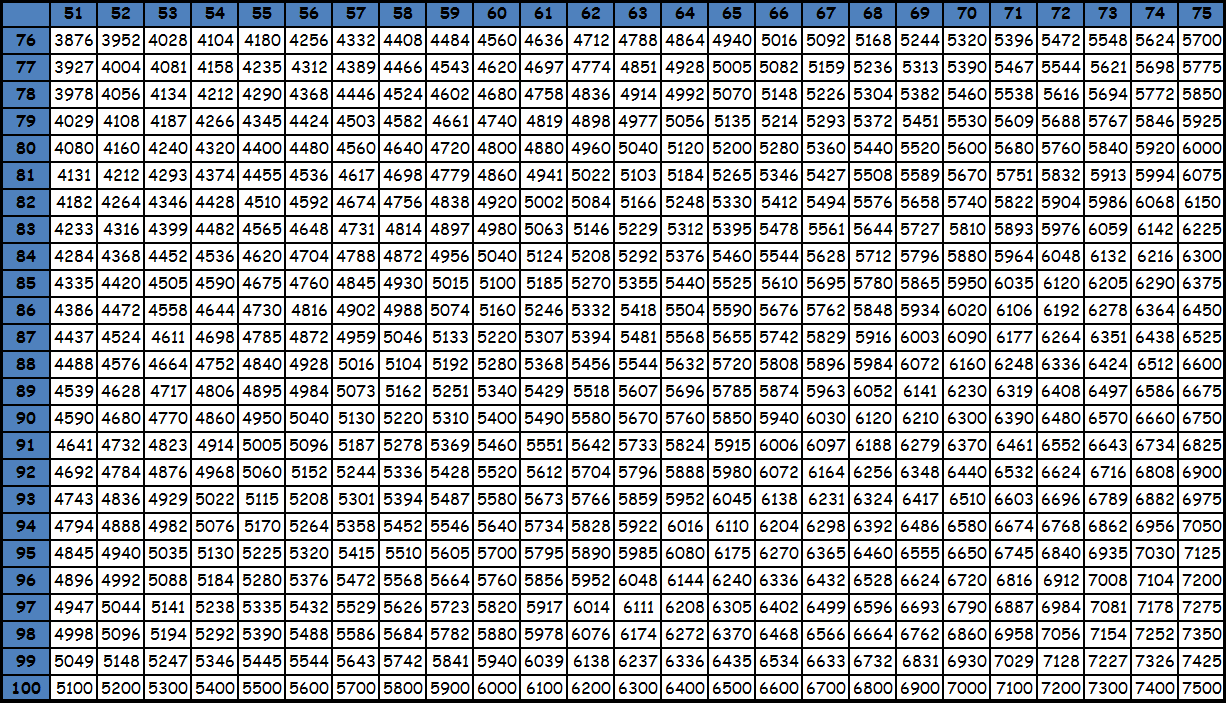
tablica-umnozheniya.ru
Правильная таблица умножения — офигеть: wod_1958 — LiveJournal
Ни о каком абстрактном мышлении здесь не может быть и речи — отвлекает всё, надо напрягаться даже чтобы просто прочитать. Но не будем сурово осуждать всех творцов, они хотели как лучше, а получилось как всегда.
Вместо злобствования попробуем немного поколдовать над всем известным, казалось бы простейшим предметом и последовательно очистить зерна истины от плевел маразма улучшательства.
Для начала убираем лишние краски, картинки, искажения и получаем обычные колонки примеров умножения:
Затем по принципу соблюдения необходимых и достаточных условий, отсекаем лишнее как скульпторы: все примеры умножения на 1 и 10 как элементарные и все повторы. Последнее очень важно, ведь при механическом запоминании следует бойкий ответ 6х8=48, а вот 8х6= уже вызывает заминку либо ошибку. При исключении повторов такое нереально, поскольку уже сама система подачи материала заставляет понять что это одно и то же. Кроме того, психологически облегчает учёбу не только снижение числа примеров со 100 до 36, но и последовательное уменьшение их количества в колонках:
Именно такой, сокращенный вариант (правда с колонкой 1 х …= ) можно было увидеть на обложках школьных тетрадей до 1970-х гг. Несомненно, можно остановиться на этом для удобства механического запоминания, но понимания математики оно не добавит. Поэтому двигаемся дальше.
Внимательный читатель наверное заметил, что до сих пор мы говорили о ПРИМЕРАХ умножения, а не о ТАБЛИЦЕ умножения.
Смотрим как выглядит настоящая, легкая, удобная для запоминания таблица умножения с полным и правильным названием: таблица умножения И ДЕЛЕНИЯ, поскольку множители одновременно являются и делителями. Хорошо заметна симметрия таблицы из-за выделения идущих по диагонали квадратов чисел:
историческое название «таблица Пифагора»
а так выглядела в древности таблица умножения у шумеров:
Делаем последнюю концептуальную трансформацию — начинаем таблицу умножения не сверху, а снизу. Почему? Во-первых, это интуитивно понятнее: ниже — меньше, выше — больше, а направление слева направо сохраняется как совпадающее с направлением письма слева — меньше, затем направо — больше. Во-вторых … расскажем чуть позднее.
Правильную таблицу умножения можно дать ученику и в готовом виде, но лучше всего если он сам её составит. Да-да. Это вполне доступно даже первокласснику!
Рисуем сетку и нумеруем ряды и столбцы с 1 до 9 — это соответствует примерам умножения на 1, они же будут выполнять функции сомножителя/кратности/во сколько раз.
Затем учеником заполняются ряд и столбец с 2 путем прибавления числа 2 для каждой последующей клеточки, затем ряд и столбец с 3 и так далее, получается простая таблица умножения:
Что это даёт?
Уже с начальной школы ученик привыкает к табличной форме, с которой ему потом придется часто встречаться, интуитивно понимает, что таблицы создаются как удобный и концентрированный справочный материал, часть из которого надо знать наизусть для удобства применения.
Поначалу для удобства пользования таблицей лучше пользоваться «уголком» для выделения строк и столбцов — вырезаем квадрат с одного угла чистого тетрадного листа. Привычка координатного поиска образуется достаточно быстро.
При таком подходе не нужно тупо механически запоминать колонки примеров умножения, а сразу можно дать пользоваться всей таблицей. Пусть она лежит перед глазами в помощь решению примеров и через некоторое время тренировок запоминание придет само, в неё ученик будет заглядывать все реже и реже.
Таблица должна стать тем же, чем она была изначально — помощью в работе. Упор всегда и везде должен быть не на запоминание, а на понимание и знание где можно найти справочный материал и как им пользоваться.
При самостоятельном заполнении таблицы умножения построчно сразу становится очевидным что умножение — это всего лишь многоКРАТНОЕ сложение, и соответственно деление — это многоКРАТНОЕ вычитание, поэтому легко приходит понимание принципиальной разницы выражений «на сколько больше/меньше» и во сколько раз больше/меньше». Это очень важно для последующего составления уравнений по условиям задач.
Выделение штриховкой или цветом диагонали (квадратов чисел) ясно показывает симметричность таблицы, т.е. равнозначность последовательности сомножителей и здесь избыточность материала играет в сторону закрепления его (повторение — мать учения) и самостоятельного выявления такой закономерности.
Уже потом, когда потребуется в процессе обучения, дети узнАют сколько полезного и интересного связано со знакомой с первого класса простенькой табличкой. Подобно Журдену из «Мещанина во дворянстве» Ж.Б. Мольера, который с удивлением узнал что он говорит прозой, детям надо будет только добавить новую терминологию и новые выводы.
Например, им будут говорить уже не просто о втором сомножителе или кратности сложения, а назовут его коэффициентом.
Каждая строка и столбец таблицы представляют из себя арифметическую прогрессию, от которой легко переходим уже к геометрической прогрессии, факториалам и прочим будто бы сложностям.
Если выделить любой прямоугольник на такой таблице, то в правом верхнем углу его будет указана площадь (чудо!), т.е. таким образом демонстрируется что алгебра и геометрия — это всего лишь разные способы отображения общих закономерностей единой науки математики. Другими словами, наглядно показывается что произведение чисел соответствует площади прямоугольника, а квадрат числа — это действительно квадрат (соответственно для куба надо рисовать третью координату). А отсюда легко переходим к решению геометрических задач алгебраическими способами и наоборот — смотря что удобнее.
Понимание графиков с осями Х и Y, названиями «абсцисса» и «ордината» уже не вызовет затруднений — это будет привычная с начальных классов форма представления материала, надо только дорисовать стрелочки. И… объяснить чем отличаются кардинальные числа от ординальных (они же количественные и порядковые соответственно).В конце-концов и понимание интеграла как суммы бесконечно малых величин исходит именно из понимания сути умножения натуральных чисел (и опять геометрические аналоги — площадь на криволинейной трапеции на графике функции), иначе интегрирование будет тупо восприниматься как заученные механические действия при обнаружении хитрой закорючки в виде длинной буквы S.
wod-1958.livejournal.com
Настоящая таблица умножения — Мастерок.жж.рф — LiveJournal
Ну так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде всю жизнь на тетрадях была таблица умножения.
Что не так-то? Есть мнение, что это очень вредная таблица умножения, а существует и настоящая.
Вот она …
По-другому ее называют «таблица Пифагора».
Верхнюю и левую колонки можно не брать, только основной прямоугольник. Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок не будет рассматривать выписанные столбиками примеры. Ни один ребенок не сможет найти в выписанных примерах интересные фишки и закономерности.
И вообще, когда учитель говорит: «Выучи таблицу умножения», — а ребенок даже перед собой таблицы не видит, он сразу понимает, что математика — это такая наука, где обычные вещи названы по-другому и надо много-много зубрить, а понять ничего невозможно.
Чем же «таблица» лучше?
— Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.
— Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение — просто таблица.
— В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос «семью восемь» он никогда не ответит «55», ведь числа 55 вообще в таблице нет и не было!
Запоминать столбики примеров способны только дети с аномальной памятью. В «таблице» надо запоминать гораздо меньше.
Например: числа, симметричные относительно диагонали, равны. Людской мозг просто настроен искать симметрию, и если ее находит и замечает, очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется.

Понимаете, ребенок замечает это сам! А то, что человек придумал сам, он запомнит навсегда, в отличие от того, что он зазубрил или ему сказали.
А ведь были же и правильные тетради:
Еще что нибудь интересного для вас: замечали ли вы, что с возрастом время летит все быстрее?, а вот Известные фразы, вырванные из контекста. Не забывайте, что «Мертвая» симка дорого обходится и вот Законы, которые защищают вас в магазине и Реальные размеры стран на карте
Это копия статьи, находящейся по адресу http://masterokblog.ru/?p=36153.masterok.livejournal.com
Новая модель таблицы умножения — Наглядное образование
 Для усвоения классической таблицы умножения используется, как правило, один способ – механическое запоминание («зубрежка»). Даже если для этого применяются игры или стихи, они также основаны на косвенном запоминании.
Для усвоения классической таблицы умножения используется, как правило, один способ – механическое запоминание («зубрежка»). Даже если для этого применяются игры или стихи, они также основаны на косвенном запоминании.
«Зубрежка» таблицы умножения может растянуться на долгие месяцы, а для кого-то так и останется на всю жизнь не до конца решенной задачей. Механическое запоминание таблицы умножения является тем самым «камнем преткновения», когда дети принимают решение что они не «математики», а «гуманитарии», а это в дальнейшем ограничивает круг выбираемых профессий и не дает полноценно реализовать себя.
Если мы рассмотрим Классическую таблицу умножения и таблицу Пифагора, то увидим, что кроме как, через «зубрежку», иных способов запоминания таблицы нет. Значит, нам нужно создать новую модель таблицы умножения, чтобы получить возможность осмысленного получения произведений.
Ведь даже используя «зубрежку», для запоминания умножения на «один», мы используем простое известное всем правило. Такое правило помогает детям за минуту выучить весь «столбик». А что если создать подобные правила счета и для других случаев умножения? Тогда мы сможем облегчить и ускорить усвоение таблицы умножения в разы. Новая модель таблицы умножения позволяет это сделать.
Компоненты умножения
Вспомним компоненты умножения.

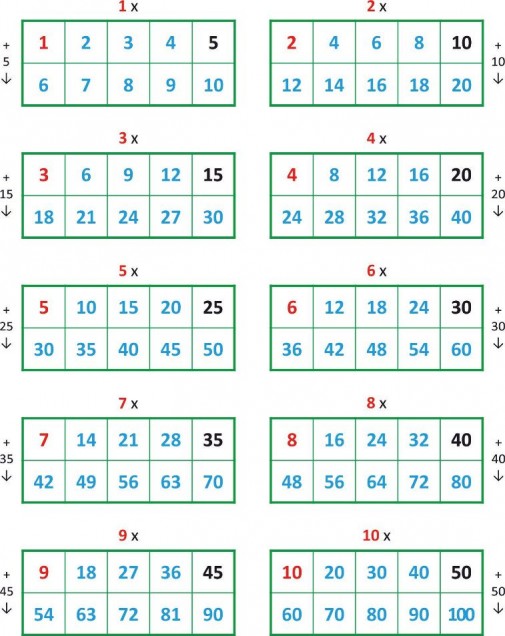
Глобальная таблица умножения
Это новая модель таблицы умножения. В этой таблице есть все компоненты умножения – они «скрыты» в ячейках таблицы. Попробуйте найти их самостоятельно. Далее будет описание.
Строение таблицы умножения
Первый множитель – всегда в первой ячейке.
Второй множитель – это всегда числа от 1 до 10 (здесь заменены на номера ячеек).
Произведения – расставлены в ячейках по порядку.
Межа – что это такое, об этом будет сказано ниже.
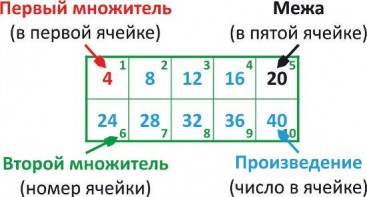
Закономерности построения таблицы умножения
Прежде чем читать дальше, вернитесь к новой модели таблицы умножения и попробуйте найти самостоятельно две закономерности построения этой таблицы. Обратите внимание на разницу между соседними ячейками по вертикали и соседними ячейками по горизонтали.
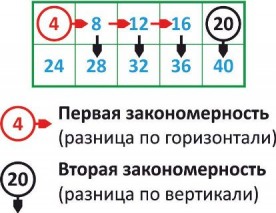
По сути, такое строение таблицы позволяет вспомнить любое произведение даже если оно было забыто, чего нельзя достичь, если учить таблицу умножения с помощью «зубрежки».
Правила сокращенного счета
Нам важна вторая закономерность, которая называется «межа» и позволяет быстро выучить, по сути половину таблицы. Если ребенок знает умножение до 5, то прибавляя межу, он может выучить оставшуюся часть таблицы. Но и в таком случае, часть таблицы нужно «вызубрить», а «зубрежка» не наш метод.
Во время тестирования новой методики, были созданы правила сокращенного счета и выработана определенная последовательность усвоения таблицы умножения. Ребенок самостоятельно получает произведения в такой последовательности и таким образом усваивает табличное умножение. По сути, таким образом табличное умножение можно усвоить за несколько часов. Но информация из кратковременной памяти в долговременную переходит в течение одних суток. Поэтому лучше усваивать не больше двух «столбиков» в день.

Полное описание правил сокращенного счета есть в методике по усвоению и в правилах к игре «Умножайка».
Деление
Эта же таблица является и таблицей деления. Деление – обратный процесс умножения.
Компоненты деления
Вспомним компоненты деления.

Строение таблицы деления
Делимое = Произведение
Делитель = Первый множитель
Частное = Второй множитель
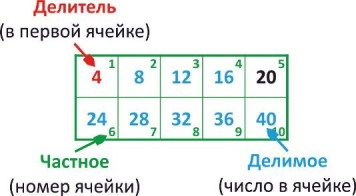
Усвоение деления
Деление рекомендуется усваивать после усвоения таблицы умножения. И делать это лучше в игре «Умножайка». Краткая суть состоит в том, что ребенок берет фишку с делимым, вспоминает какие у него делитель и частное и ставит фишку в нужное место игры, самостоятельно собирая «матрицу» всей таблицы.
Новый способ «Осмысленного усвоения таблицы умножения» позволяет не только быстро выучить таблицу умножения, но и вспомнить любое произведение, даже если оно было забыто. Легкость усвоения таблицы умножения избавляет детей от «математической тревожности», позволяет полюбить не только математику, но и другие школьные предметы.
Повышение успеваемости,
Легкое, быстрое и своевременное усвоение таблицы умножения помогает ребенку избежать «математической тревожности», в дальнейшем повышает его успеваемость по математике, геометрии, информатике, алгебре, физике, химии. «Математики» получают более высокие баллы на экзаменах, поступают в более престижные ВУЗы.
Узнать больше
Приобрести игру Пройти обучение
Поделиться
xn--80ace7a3b4aza.xn--p1ai
Настоящая таблица умножения — Мастерок.жж.рф — LiveJournal

Ну так чем же эта тетрадь плоха? Ничего не подозревающий родитель видит, что на тетради таблица умножения. Вроде всю жизнь на тетрадях была таблица умножения.
Что не так-то? Есть мнение, что это очень вредная таблица умножения, а существует и настоящая.
Вот она …
По-другому ее называют «таблица Пифагора».
Верхнюю и левую колонки можно не брать, только основной прямоугольник. Во-первых, это таблица. Во-вторых, она интересная!
Ни один ребенок не будет рассматривать выписанные столбиками примеры. Ни один ребенок не сможет найти в выписанных примерах интересные фишки и закономерности.
И вообще, когда учитель говорит: «Выучи таблицу умножения», — а ребенок даже перед собой таблицы не видит, он сразу понимает, что математика — это такая наука, где обычные вещи названы по-другому и надо много-много зубрить, а понять ничего невозможно.
Чем же «таблица» лучше?
— Во-первых, в ней нет мусора и информационного шума в виде левой части примеров.
— Во-вторых, над ней можно подумать. Тут даже нигде не написано, что это умножение — просто таблица.
— В-третьих, если она постоянно под рукой и ребенок на нее постоянно натыкается, он волей-неволей начинает запоминать эти числа. В частности, на вопрос «семью восемь» он никогда не ответит «55», ведь числа 55 вообще в таблице нет и не было!
Запоминать столбики примеров способны только дети с аномальной памятью. В «таблице» надо запоминать гораздо меньше.
Кроме того, ребенок автоматом ищет закономерности. И сам самостоятельно их находит. Такие закономерности находят даже дети, еще не умеющие умножать.
Например: числа, симметричные относительно диагонали, равны. Людской мозг просто настроен искать симметрию, и если ее находит и замечает, очень радуется. А что это означает? Это означает, что от перестановки мест сомножителей произведение не меняется.
Понимаете, ребенок замечает это сам! А то, что человек придумал сам, он запомнит навсегда, в отличие от того, что он зазубрил или ему сказали.
А ведь были же и правильные тетради:
источник
Еще что нибудь интересного для вас: замечали ли вы, что с возрастом время летит все быстрее?, а вот Известные фразы, вырванные из контекста. Не забывайте, что «Мертвая» симка дорого обходится и вот Законы, которые защищают вас в магазине и Реальные размеры стран на карте
masterok.livejournal.com
Таблица умножения до 20 | Сайт о таблице умножения
1 x 1 = 1
1 x 2 = 2
1 x 3 = 3
1 x 4 = 4
1 x 5 = 5
1 x 6 = 6
1 x 7 = 7
1 x 8 = 8
1 x 9 = 9
1 x 10 = 10
1 x 11 = 11
1 x 12 = 12
1 x 13 = 13
1 x 14 = 14
1 x 15 = 15
1 x 16 = 16
1 x 17 = 17
1 x 18 = 18
1 x 19 = 19
1 x 20 = 20
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
2 x 11 = 22
2 x 12 = 24
2 x 13 = 26
2 x 14 = 28
2 x 15 = 30
2 x 16 = 32
2 x 17 = 34
2 x 18 = 36
2 x 19 = 38
2 x 20 = 40
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27
3 x 10 = 30
3 x 11 = 33
3 x 12 = 36
3 x 13 = 39
3 x 14 = 42
3 x 15 = 45
3 x 16 = 48
3 x 17 = 51
3 x 18 = 54
3 x 19 = 57
3 x 20 = 60
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
4 x 9 = 36
4 x 10 = 40
4 x 11 = 44
4 x 12 = 48
4 x 13 = 52
4 x 14 = 56
4 x 15 = 60
4 x 16 = 64
4 x 17 = 68
4 x 18 = 72
4 x 19 = 76
4 x 20 = 80
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
5 x 9 = 45
5 x 10 = 50
5 x 11 = 55
5 x 12 = 60
5 x 13 = 65
5 x 14 = 70
5 x 15 = 75
5 x 16 = 80
5 x 17 = 85
5 x 18 = 90
5 x 19 = 95
5 x 20 = 100
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
6 x 11 = 66
6 x 12 = 72
6 x 13 = 78
6 x 14 = 84
6 x 15 = 90
6 x 16 = 96
6 x 17 = 102
6 x 18 = 108
6 x 19 = 114
6 x 20 = 120
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 x 10 = 70
7 x 11 = 77
7 x 12 = 84
7 x 13 = 91
7 x 14 = 98
7 x 15 = 105
7 x 16 = 112
7 x 17 = 119
7 x 18 = 126
7 x 19 = 133
7 x 20 = 140
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
8 x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
8 x 10 = 80
8 x 11 = 88
8 x 12 = 96
8 x 13 = 104
8 x 14 = 112
8 x 15 = 120
8 x 16 = 128
8 x 17 = 136
8 x 18 = 144
8 x 19 = 152
8 x 20 = 160
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
9 x 11 = 99
9 x 12 = 108
9 x 13 = 117
9 x 14 = 126
9 x 15 = 135
9 x 16 = 144
9 x 17 = 153
9 x 18 = 162
9 x 19 = 171
9 x 20 = 180
10 x 1 = 10
10 x 2 = 20
10 x 3 = 30
10 x 4 = 40
10 x 5 = 50
10 x 6 = 60
10 x 7 = 70
10 x 8 = 80
10 x 9 = 90
10 x 10 = 100
10 x 11 = 110
10 x 12 = 120
10 x 13 = 130
10 x 14 = 140
10 x 15 = 150
10 x 16 = 160
10 x 17 = 170
10 x 18 = 180
10 x 19 = 190
10 x 20 = 200
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
11 x 7 = 77
11 x 8 = 88
11 x 9 = 99
11 x 10 = 110
11 x 11 = 121
11 x 12 = 132
11 x 13 = 143
11 x 14 = 154
11 x 15 = 165
11 x 16 = 176
11 x 17 = 187
11 x 18 = 198
11 x 19 = 209
11 x 20 = 220
12 x 1 = 12
12 x 2 = 24
12 x 3 = 36
12 x 4 = 48
12 x 5 = 60
12 x 6 = 72
12 x 7 = 84
12 x 8 = 96
12 x 9 = 108
12 x 10 = 120
12 x 11 = 132
12 x 12 = 144
12 x 13 = 156
12 x 14 = 168
12 x 15 = 180
12 x 16 = 192
12 x 17 = 204
12 x 18 = 216
12 x 19 = 228
12 x 20 = 240
13 x 1 = 13
13 x 2 = 26
13 x 3 = 39
13 x 4 = 52
13 x 5 = 65
13 x 6 = 78
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
13 x 11 = 143
13 x 12 = 156
13 x 13 = 169
13 x 14 = 182
13 x 15 = 195
13 x 16 = 208
13 x 17 = 221
13 x 18 = 234
13 x 19 = 247
13 x 20 = 260
14 x 1 = 14
14 x 2 = 28
14 x 3 = 42
14 x 4 = 56
14 x 5 = 70
14 x 6 = 84
14 x 7 = 98
14 x 8 = 112
14 x 9 = 126
14 x 10 = 140
14 x 11 = 154
14 x 12 = 168
14 x 13 = 182
14 x 14 = 196
14 x 15 = 210
14 x 16 = 224
14 x 17 = 238
14 x 18 = 252
14 x 19 = 266
14 x 20 = 280
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
15 x 5 = 75
15 x 6 = 90
15 x 7 = 105
15 x 8 = 120
15 x 9 = 135
15 x 10 = 150
15 x 11 = 165
15 x 12 = 180
15 x 13 = 195
15 x 14 = 210
15 x 15 = 225
15 x 16 = 240
15 x 17 = 255
15 x 18 = 270
15 x 19 = 285
15 x 20 = 300
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 x 6 = 96
16 x 7 = 112
16 x 8 = 128
16 x 9 = 144
16 x 10 = 160
16 x 11 = 176
16 x 12 = 192
16 x 13 = 208
16 x 14 = 224
16 x 15 = 240
16 x 16 = 256
16 x 17 = 272
16 x 18 = 288
16 x 19 = 304
16 x 20 = 320
17 x 1 = 17
17 x 2 = 34
17 x 3 = 51
17 x 4 = 68
17 x 5 = 85
17 x 6 = 102
17 x 7 = 119
17 x 8 = 136
17 x 9 = 153
17 x 10 = 170
17 x 11 = 187
17 x 12 = 204
17 x 13 = 221
17 x 14 = 238
17 x 15 = 255
17 x 16 = 272
17 x 17 = 289
17 x 18 = 306
17 x 19 = 323
17 x 20 = 340
18 x 1 = 18
18 x 2 = 36
18 x 3 = 54
18 x 4 = 72
18 x 5 = 90
18 x 6 = 108
18 x 7 = 126
18 x 8 = 144
18 x 9 = 162
18 x 10 = 180
18 x 11 = 198
18 x 12 = 216
18 x 13 = 234
18 x 14 = 252
18 x 15 = 270
18 x 16 = 288
18 x 17 = 306
18 x 18 = 324
18 x 19 = 342
18 x 20 = 360
19 x 1 = 19
19 x 2 = 38
19 x 3 = 57
19 x 4 = 76
19 x 5 = 95
19 x 6 = 114
19 x 7 = 133
19 x 8 = 152
19 x 9 = 171
19 x 10 = 190
19 x 11 = 209
19 x 12 = 228
19 x 13 = 247
19 x 14 = 266
19 x 15 = 285
19 x 16 = 304
19 x 17 = 323
19 x 18 = 342
19 x 19 = 361
19 x 20 = 380
20 x 1 = 20
20 x 2 = 40
20 x 3 = 60
20 x 4 = 80
20 x 5 = 100
20 x 6 = 120
20 x 7 = 140
20 x 8 = 160
20 x 9 = 180
20 x 10 = 200
20 x 11 = 220
20 x 12 = 240
20 x 13 = 260
20 x 14 = 280
20 x 15 = 300
20 x 16 = 320
20 x 17 = 340
20 x 18 = 360
20 x 19 = 380
20 x 20 = 400
По запросам в Интернете часто предлагают сокращенный вариант таблицы до 20, в котором отсутствует часть самых сложных примеров.
Сокращенная таблица умножения до 20
1 x 1 = 1
1 x 2 = 2
1 x 3 = 3
1 x 4 = 4
1 x 5 = 5
1 x 6 = 6
1 x 7 = 7
1 x 8 = 8
1 x 9 = 9
1 x 10 = 10
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27
3 x 10 = 30
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
4 x 9 = 36
4 x 10 = 40
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
5 x 9 = 45
5 x 10 = 50
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 x 10 = 70
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
8 x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
8 x 10 = 80
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
10 x 1 = 10
10 x 2 = 20
10 x 3 = 30
10 x 4 = 40
10 x 5 = 50
10 x 6 = 60
10 x 7 = 70
10 x 8 = 80
10 x 9 = 90
10 x 10 = 100
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
11 x 7 = 77
11 x 8 = 88
11 x 9 = 99
11 x 10 = 110
12 x 1 = 12
12 x 2 = 24
12 x 3 = 36
12 x 4 = 48
12 x 5 = 60
12 x 6 = 72
12 x 7 = 84
12 x 8 = 96
12 x 9 = 108
12 x 10 = 120
13 x 1 = 13
13 x 2 = 26
13 x 3 = 39
13 x 4 = 52
13 x 5 = 65
13 x 6 = 78
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
14 x 1 = 14
14 x 2 = 28
14 x 3 = 42
14 x 4 = 56
14 x 5 = 70
14 x 6 = 84
14 x 7 = 98
14 x 8 = 112
14 x 9 = 126
14 x 10 = 140
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
15 x 5 = 75
15 x 6 = 90
15 x 7 = 105
15 x 8 = 120
15 x 9 = 135
15 x 10 = 150
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 x 6 = 96
16 x 7 = 112
16 x 8 = 128
16 x 9 = 144
16 x 10 = 160
17 x 1 = 17
17 x 2 = 34
17 x 3 = 51
17 x 4 = 68
17 x 5 = 85
17 x 6 = 102
17 x 7 = 119
17 x 8 = 136
17 x 9 = 153
17 x 10 = 170
18 x 1 = 18
18 x 2 = 36
18 x 3 = 54
18 x 4 = 72
18 x 5 = 90
18 x 6 = 108
18 x 7 = 126
18 x 8 = 144
18 x 9 = 162
18 x 10 = 180
19 x 1 = 19
19 x 2 = 38
19 x 3 = 57
19 x 4 = 76
19 x 5 = 95
19 x 6 = 114
19 x 7 = 133
19 x 8 = 152
19 x 9 = 171
19 x 10 = 190
20 x 1 = 20
20 x 2 = 40
20 x 3 = 60
20 x 4 = 80
20 x 5 = 100
20 x 6 = 120
20 x 7 = 140
20 x 8 = 160
20 x 9 = 180
20 x 10 = 200
tablica-umnozhenia.ru
Логический способ изучения таблицы умножения
Это один из лучших способов изучения таблицы умножения. С его помощью ребенок не только получит практические навыки по таблице, но и научится рассуждать и анализировать. При этом количество примеров для заучивания сводится к минимуму.
Всего в полной таблице умножения от 1 до 10 насчитывается 100 примеров. Это довольно много, если пытаться просто выучить их все. В конце статьи будет показано как сильно уменьшится число примеров для запоминания при применении логического подхода.
Суть метода
Многие примеры из таблицы умножения можно вычислять, основываясь на наборе правил. При этом можно выделить 2 вида правил:
- Основные, применимые ко всей таблице.
- Специальные, касающиеся отдельных столбцов.
Основные правила
Основных правил всего 2:
-
«Переместительное свойство» – от перемены мест множителей произведение не меняется. Нужно, чтобы все примеры ребенок «разворачивал» в уме в правильном порядке, то есть меньшее число умножается на большее. Тогда сложный пример 9 * 2 превратится в пример 2 * 9, который значительно проще.
Помимо этого, сокращается количество примеров, так как убираются дубликаты.
- Умножение – это многократное сложение. Любое умножение можно заменить сложением или вычитанием.
Специальные правила
- Умножение на 1
Самое простое, что может быть. Число не меняется при умножении на один. Правило легко объяснить, легко запомнить. - Умножение на 10
Еще одно очень простое правило. При умножении на 10, к концу числа добавляется 0, на этом все. - Умножение на 2
Умножение на 2 заменяем сложением. Сложение двух чисел на момент изучения таблицы не вызывает сложностей у большинства учеников. - Умножение на 3
Начальные примеры умножения на 3, а именно до 5, еще легко можно заменить тройным сложением. - Умножение на 5
Умножение на 5 всегда заканчивается на 5 или на 0. Благодаря этому легко определить весь столбец. При этом можно попробовать при умножении на 8 и 9 не складывать, а вычитать из 5 * 10 = 50 нужное количество раз. - Умножение на 9
Интересно умножение на 9. Такое умножение нужно заменять вычитанием числа из легкого умножения на 10. То есть 8 * 9, это 8 * 10 = 80 и 80 – 8 = 72.
Применяя все правила, останется выучить следующие примеры:
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
7 x 7 = 49
7 x 8 = 56
8 x 8 = 64
Или всего 14 примеров, что куда меньше чем 100.
Плюсы метода
- Сильно уменьшает объем запоминаемой информации.
- Помогает понять умножение.
- В отличие от таблицы Пифагора дает реальные навыки определения произведения без использования таблиц.
- Развивает мышление.
Минусы метода
- Метод подойдет не всем ученикам. В зависимости от склонностей к математике, возможно ребенок усвоит не все правила.
tablica-umnozhenia.ru